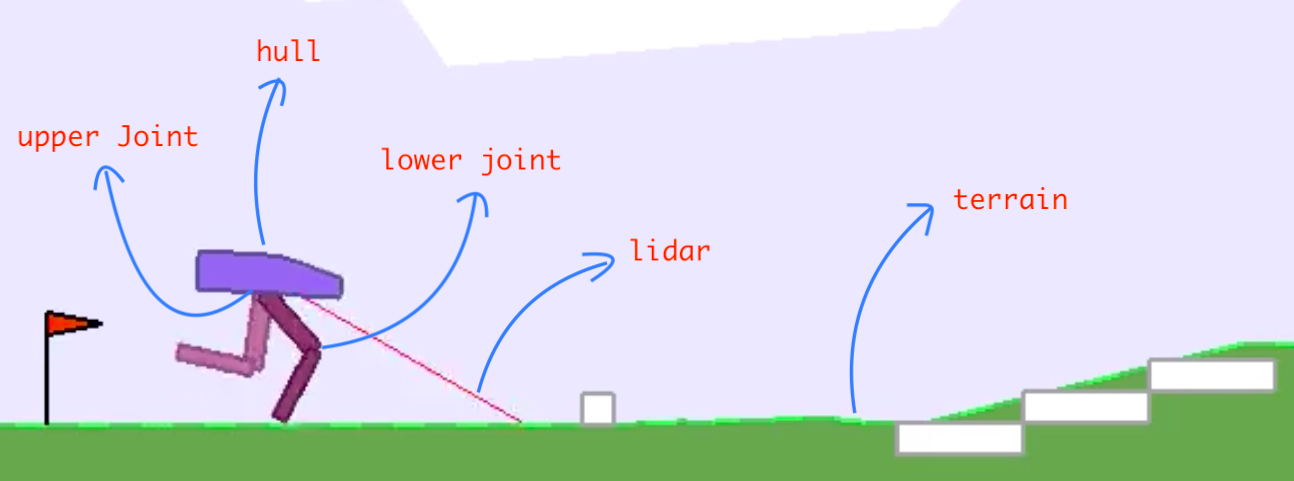
In this article we look at the classical bipedal walker environment. This is a simple 4-joint walker robot environment. There are two versions: the normal one, where the robot faces a slightly uneven terrain, and the hardcore one, with ladders, stumps, pitfalls. We cover the normal one in this article and the hardcore version in the next one.
To solve the normal version, you need to get 300 points in 1600 time steps.
The state space consists of hull angle speed, angular velocity, horizontal speed, vertical speed, position of joints and joints angular speed, legs contact with ground, and 10 lidar rangefinder measurements. There are no coordinates in the state vector. Actions are motor speed values in the [-1, 1] range for each of the 4 joints at both hips and knees.
Reward is given for moving forward, totaling 300+ points up to the far end. If the robot falls, it gets -100. Applying motor torque costs a small amount of points. A more optimal agent will get a better score.
The method we will use is called Augmented Random Search, presented in the paper Simple random search provides a competitive approach to reinforcement learning, published in 2018. The authors aim to present a simple baseline for reinforcement learning by using random search for a parametrized policy $\pi_\theta : \mathbb{R}^n \rightarrow \mathbb{R}^p \rightarrow \mathbb{R}^m$, where $\theta \in \mathbb{R}^p$ are the policy parameters. The basic idea is to optimize over those policy parameters directly instead of doing so in the action space and is an extension of the classical random search method.
Random Search is one of the simplest and oldest optimization methods for derivative-free optimization. Given
- a step size $\alpha$,
- the number of directions samples per iteration $N$, and
- the standard deviation of the exploration noise $\nu$,
at each step $j$ it chooses a direction uniformly at random on the sphere in the parameter space, and then optimizes the function along this direction. That is, it samples $\delta_1, \delta_2, \ldots, \delta_N$, each of them of same size as $\theta_j$, using a standard normal distribution, and collects the corresponding rewards using the policies
\[\begin{aligned} \pi_{\theta,j,+}(x) & = \pi_{\theta_j + \nu \delta_k}(x) \\ \pi_{\theta,j,-}(x) & = \pi_{\theta_j - \nu \delta_k}(x) \end{aligned}\]with $k \in {1, 2, \ldots, N}$. The update step is then \(\theta_{j + 1} = \theta_j + \frac{\alpha}{N} \sum{k=1}^N \left[ \pi_{j,k,+}(x) - \pi_{j,k,-}(x) \right] \delta_k.\) The procedure is repeated until some ending conditions are satisfied after setting $j \leftarrow j = 1$.
The augmented version has more parameters: a matrix $M_0 =0 \in \mathbb{R}^{p \times n}$, a vector $\mu_0 = 0 \in \mathbb{R}^n$, a matrix $\Sigma_0 = I_n \in \mathbb{R}^{n \times n}$, and the number of top-performing directions to use $b$, possibly set equal to $N$. The paper assumes linear policies, that is we simply have
\[\pi_j(x) = M_j x,\]that is
\[\begin{aligned} \pi_{j, k, +}(x) & = (M_j + \nu \delta_k) x \\ \pi_{j, k, }(x) & = (M_j - \nu \delta_k) x \end{aligned}\]for the V1 version of the algorith, or
\[\begin{aligned} \pi_{j, k, +}(x) & = (M_j + \nu \delta_k) \operatorname{diag}(\Sigma_j)^{-1/2} (x - \mu_j) \\ \pi_{j, k, }(x) & = (M_j - \nu \delta_k) \operatorname{diag}(\Sigma_j)^{-1/2} (x - \mu_j) \end{aligned}\]for the V2 version and $k \in {1, 2, \ldots, N}$. The code in this notebook implementes the V1 version.
Once the episodes (or rollouts) are collected, we sort the directions $\delta_k$ by the maximum difference in reward and denote by $\delta_{(k)}$ the $k$-largest direction and by $\pi_{j, (k), +}$ and $\pi_{j, (k), -}$ the corresponding policies. The update step is
\[M_{j + 1} = M_j + \frac{\alpha}{b \sigma_R} \sum_{k=1}^b \left[ \pi_{j,(k),+}(x) - \pi_{j,(k),-}(x) \right] \delta_{(k)}.\]where $\sigma_R$ is the standard deviation of the $b$ rewards used in the update step.
The computations are run on an Ubuntu Linux computer, with the following conda environment:
conda create --name bipedal-walker python==3.7 --no-default-packages -y
conda activate bipedal-walker
conda install swig -y
pip install gym
pip install torch
pip install gym[box2d]
sudo apt-get install xvfb
sudo apt-get install freeglut3-dev
pip install jupyterlab
pip install tensorboard
pip install pyvirtualdisplay
pip install matplotlib
import os
import numpy as np
import gym
from gym import wrappers
from torch.utils.tensorboard import SummaryWriter
import logging
logging.basicConfig(
level=logging.DEBUG,
format='[%(asctime)s] %(message)s',
filename=('bipedal-walker.log'),
)
logger = logging.getLogger('pytorch')
logger.info('Start')
ENV_NAME = 'BipedalWalker-v3'
LEARNING_RATE = 0.02
NUM_DELTAS = 32
NUM_BEST_DELTAS = 32
NOISE = 0.05
SEED = 1
RECORD_EVERY = 50
EPISODE_LENGTH = 1_600
NUM_STEPS = 1_000
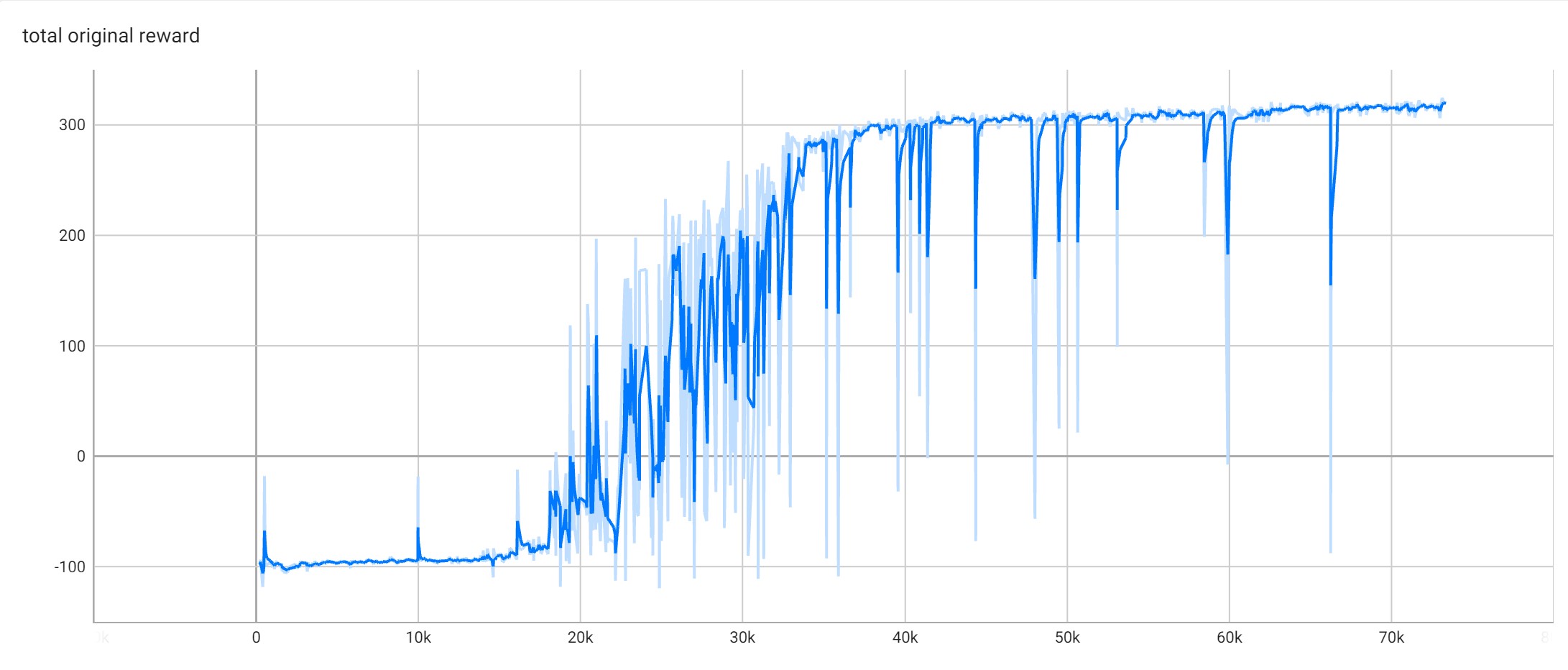
The small utility class Logger does two things: the first one, as its name suggests, is to log the episodes (to tensorboard); the second one is to modify the reward by enforcing it to be at least -1. This small trick turns out to be quite beneficial, as the agent is not punished too harshily when falls and can therefore explore more freely.
class Logger(gym.Wrapper):
def __init__(self, env: gym.Env):
super().__init__(env)
self._reset_params()
self._writer = SummaryWriter(log_dir='./data')
self._num_episodes = 0
def step(self, action):
observation, reward, terminated, truncated, info = self.env.step(action)
self._episode_length += 1
self._total_original_reward += reward
# limit the reward seen by the learner
reward = max(reward, -1)
self._total_reward += reward
if terminated or truncated:
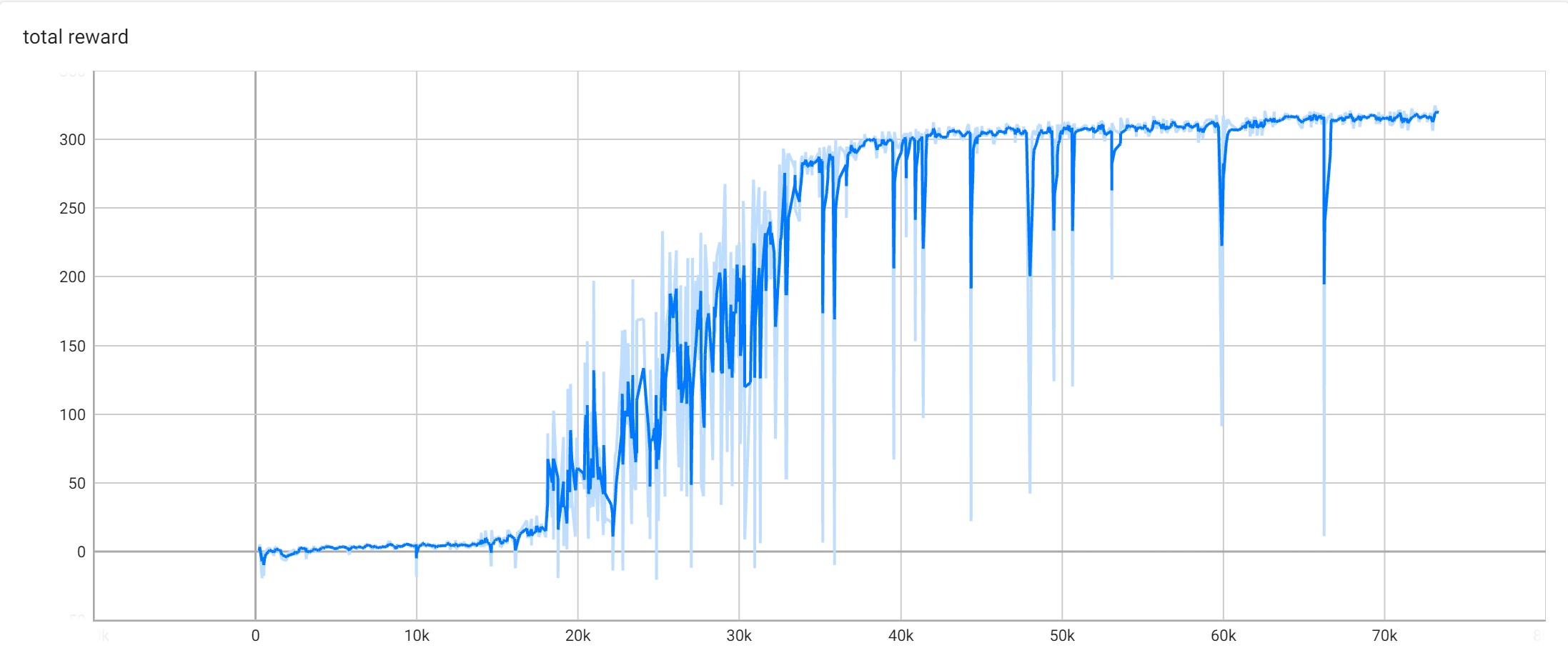
self._writer.add_scalar('total reward', self._total_reward, self._num_episodes)
self._writer.add_scalar('total original reward', self._total_original_reward, self._num_episodes)
self._writer.add_scalar('episode length', self._episode_length, self._num_episodes)
self._reset_params()
self._num_episodes += 1
return observation, reward, terminated, truncated, info
def reset(self, **kwargs):
self._reset_params()
return self.env.reset(**kwargs)
def _reset_params(self):
self._episode_length = 0
self._total_reward = 0.0
self._total_original_reward = 0.0
The Normalizer class is used to normalize the inputs. The inputs of the ARS algorithm need to be normalized, and typically this is done by taking running statistics of each of the input components, then using these statistics to do a mean/standard deviation filter (normalization) of the future inputs. This allows the algorithm to create appropriate distributions for normalizing inputs over time as it experiences more and more states, without needing prior knowledge of these distributions.
class Normalizer():
def __init__(self, num_inputs):
self.n = np.zeros(num_inputs)
self.mean = np.zeros(num_inputs)
self.mean_diff = np.zeros(num_inputs)
self.var = np.zeros(num_inputs)
def observe(self, x):
self.n += 1.0
last_mean = self.mean.copy()
self.mean += (x - self.mean) / self.n
self.mean_diff += (x - last_mean) * (x - self.mean)
self.var = (self.mean_diff / self.n).clip(min=1e-2)
def normalize(self, inputs):
obs_mean = self.mean
obs_std = np.sqrt(self.var)
return (inputs - obs_mean) / obs_std
class Policy():
def __init__(self, num_inputs, num_outputs):
self.theta = np.zeros((num_outputs, num_inputs))
def evaluate(self, input, delta = None, direction = None):
if direction is None:
return self.theta.dot(input)
elif direction == "+":
return (self.theta + NOISE * delta).dot(input)
elif direction == "-":
return (self.theta - NOISE * delta).dot(input)
def sample_deltas(self):
return [np.random.randn(*self.theta.shape) for _ in range(NUM_DELTAS)]
def update(self, rollouts, sigma_rewards):
# sigma_rewards is the standard deviation of the rewards
step = np.zeros(self.theta.shape)
for pos_reward, neg_reward, delta in rollouts:
step += (pos_reward - neg_reward) * delta
self.theta += LEARNING_RATE / (NUM_BEST_DELTAS * sigma_rewards) * step
class AugmentedRandomSearch():
def __init__(self):
np.random.seed(SEED)
self.env = gym.make(ENV_NAME)
self.env = wrappers.TimeLimit(self.env, EPISODE_LENGTH)
self.env = Logger(self.env)
self.num_inputs = self.env.observation_space.shape[0]
self.num_outputs = self.env.action_space.shape[0]
self.normalizer = Normalizer(self.num_inputs)
self.policy = Policy(self.num_inputs, self.num_outputs)
self.history = []
# Explore the policy on one specific direction and over one episode
def explore(self, direction=None, delta=None):
state, _ = self.env.reset()
done = False
sum_rewards = 0.0
while not done:
self.normalizer.observe(state)
state = self.normalizer.normalize(state)
action = self.policy.evaluate(state, delta, direction)
state, reward, done, terminated, _ = self.env.step(action)
if terminated: done = True
sum_rewards += reward
return sum_rewards
def train(self):
for step in range(NUM_STEPS):
# initialize the random noise deltas and the positive/negative rewards
deltas = self.policy.sample_deltas()
positive_rewards = [0] * NUM_DELTAS
negative_rewards = [0] * NUM_DELTAS
# play an episode each with positive deltas and negative deltas, collect rewards
for k in range(NUM_DELTAS):
positive_rewards[k] = self.explore(direction="+", delta=deltas[k])
negative_rewards[k] = self.explore(direction="-", delta=deltas[k])
# Compute the standard deviation of all rewards
sigma_rewards = np.array(positive_rewards + negative_rewards).std()
# Sort the rollouts by the max(r_pos, r_neg) and select the deltas with best rewards
scores = {k: max(r_pos, r_neg) for k,(r_pos,r_neg) in enumerate(zip(positive_rewards, negative_rewards))}
order = sorted(scores.keys(), key = lambda x: scores[x], reverse = True)[:NUM_BEST_DELTAS]
rollouts = [(positive_rewards[k], negative_rewards[k], deltas[k]) for k in order]
# Update the policy
self.policy.update(rollouts, sigma_rewards)
# Play an episode with the new weights and print the score
reward_evaluation = self.explore()
self.history.append(reward_evaluation)
logger.info(f'step: {step}, reward evaluation: {reward_evaluation}')
agent = AugmentedRandomSearch()
agent.train()
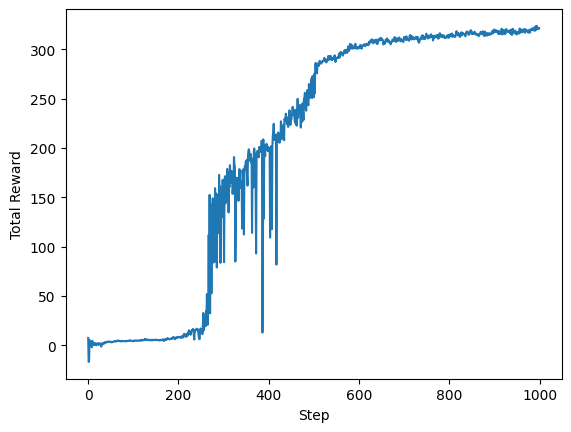
import matplotlib.pylab as plt
plt.plot(agent.history)
plt.xlabel('Step')
plt.ylabel('Total Reward')
Text(0, 0.5, 'Total Reward')
agent.env = gym.make(ENV_NAME, render_mode='rgb_array')
state, _ = agent.env.reset()
done = False
rewards = []
frames = [agent.env.render()]
while not done:
agent.normalizer.observe(state)
state = agent.normalizer.normalize(state)
action = agent.policy.evaluate(state)
state, reward, done, truncated, _ = agent.env.step(action)
if truncated: done = True
frames.append(agent.env.render())
rewards.append(reward)
if len(frames) > 3000:
break
agent.env.close()
print(f'Episode length: {len(frames)}, total reward: {sum(rewards):.2f}.')
Episode length: 995, total reward: 323.27.
from matplotlib import animation
video = np.array(frames)
total_rewards = [0] + np.cumsum(rewards).tolist()
fig, ax = plt.subplots(figsize=(4, 4))
im = ax.imshow(video[0,:,:,:])
ax.set_axis_off()
text = ax.text(10, 10, '', color='red')
plt.close() # this is required to not display the generated image
def init():
im.set_data(video[0,:,:,:])
def animate(i):
im.set_data(video[i,:,:,:])
text.set_text(f'Step {i}, total reward: {total_rewards[i]:.2f}')
return im
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=video.shape[0],
interval=100)
anim.save('bipedal-walker-video.gif', dpi=80, fps=24)
