In this article we implement Deep Q-Network (DQN), which is a very interesting method for reinforcement learning presented in this 2013 article, followed in 2015 by another publication on Nature, available for download on the DeepMind website.
This page is largely inspired from the official PyTorch tutorial, yet with the with cart pole environment. We will use the observation space that comes with the environment for a simpler problem and leave image processing for a later article.
We start with a few imports.
import torch
from torch import nn
import torch.nn.functional as F
import random
import copy
from collections import deque, namedtuple
import numpy as np
import gym
from tqdm.notebook import tnrange as trange
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
The environment is CartPole-v0. This problem is deterministic and fairly simple; as such, it can be solved without GPUs on a normal computer in a few minutes, which is quite good for experimenting.
env = gym.make('CartPole-v0')
The DQN method per se is quite unstable. The 2013 paper suggests a few approaches to stabilize the learning, the first of which is the experience replay. Experience replay was first suggested in a reinforcement learning context in 1992, see also here. The idea is to collect what the agent does through its learning phase, store it, and replay it frequently. The method is therefore in between an on-line method, that learns continuously from experience, and batch reinforcement learning, where the complete amount of experience is fixed and given a priori. The former is very slow to converge, while in the latter the agent is not allowed to interact with the system during learning and requires a policy to collect the experience. Besides, if important regions are not covered by any samples, then it is impossible for the agent to learn a good policy from the data because of the missing information. The experience replay finds a middle ground that is simple to implement and very effective.
We start with a data structure to host the transitions. It contains the current state, the action taken, the next state (or None if the state was terminal) and the reward.
Transition = namedtuple('Transition', ('state', 'action', 'next_state', 'reward'))
The first class we need to define is the experience replay itself, taken verbatim from the PyTorch website. It contains a vector, to which new experiences are appended, up to a maximum of capacity entries. After that, new entries overwrite the old ones. Method sample() returns a random sample of the given size. We need to sample randomly to avoid correlated transitions to be used at the same time. Typical values for capacity are 10’000 or 100’000, while typical values for batch_size are 128 or 256, so much smaller.
class ReplayMemory:
def __init__(self, capacity):
self.capacity = capacity
self.memory = []
self.position = 0
def push(self, *args):
if len(self.memory) < self.capacity:
self.memory.append(None)
self.memory[self.position] = Transition(*args)
self.position = (self.position + 1) % self.capacity
def sample(self, batch_size):
return random.sample(self.memory, batch_size)
def __len__(self):
return len(self.memory)
The other class is the main class: it defines the agent and incorporates the DQN logic. In the __init__() method, we start by setting the seeds to ensure reproducibility, then we create the policy and the target network, and define the replay memory object. The networks are simple sequential neural networks, generally with one hidden layer. The action, either the optimal one or a random one, is returned by get_action(); method remember() stores an new transition into the memory replay, while sync() synchronizes the policy and the target networks. The DQN logic is implemented in optimize(). The loss function is the Huber loss, which is less sensitive to outliers than then squared error loss.
The sync() method is used to align the target network with the policy network and has been suggested in the 2013 paper. The idea is to update the policy frequently yet use a slightly more ‘static’ network for the computing the Q values that are used in the loss. This reduces the instabilities and ensures smoother convergence. We also clip the gradients into $[-1, 1]$ to avoid large variations from the one step to the next.
class DQNAgent:
def __init__(self, seed, num_observations, num_actions, hidden_layer_sizes, learning_rate,
capacity, batch_size, gamma):
torch.manual_seed(seed)
env.seed(seed + 1)
env.action_space.seed(seed + 2)
np.random.seed(seed + 3)
random.seed(seed + 4)
self.num_actions = num_actions
layer_sizes = [num_observations] + list(hidden_layer_sizes) + [num_actions]
self.policy_net = self.build_network(layer_sizes)
self.target_net = self.build_network(layer_sizes)
self.target_net.load_state_dict(self.policy_net.state_dict())
self.target_net.eval()
self.optimizer = torch.optim.Adam(self.policy_net.parameters(), lr=learning_rate)
self.gamma = gamma
self.memory = ReplayMemory(capacity)
self.batch_size = batch_size
@staticmethod
def build_network(layer_sizes):
assert len(layer_sizes) > 1
layers = []
for index in range(len(layer_sizes) - 1):
linear = nn.Linear(layer_sizes[index], layer_sizes[index + 1])
act = nn.Tanh() if index < len(layer_sizes) - 2 else nn.Identity()
layers += (linear, act)
return nn.Sequential(*layers)
def get_action(self, state, epsilon):
# epsilon-greedy part, we select a random action
if torch.rand(1).item() <= epsilon:
return torch.randint(0, self.num_actions, (1,)).item()
# gradients aren't needed
with torch.no_grad():
Q_row = self.policy_net(torch.from_numpy(state).float())
Q, A = torch.max(Q_row, axis=0)
return A.item()
def remember(self, state, action, next_state, reward):
state = torch.tensor([state], dtype=torch.float, device=device)
action = torch.tensor([[action]], dtype=torch.int64, device=device)
next_state = None if next_state is None else torch.tensor([next_state], dtype=torch.float, device=device)
reward = torch.tensor([reward], dtype=torch.float, device=device)
self.memory.push(state, action, next_state, reward)
def sync(self):
self.target_net.load_state_dict(self.policy_net.state_dict())
def optimize(self):
# if we don't have enough experience yet, we don't optimize and simply return
if len(self.memory) < self.batch_size:
return np.nan
# sample for memory to create a batch of transitions
transitions = self.memory.sample(self.batch_size)
# Transpose the batch (see https://stackoverflow.com/a/19343/3343043 for
# detailed explanation). This converts batch-array of Transitions to Transition of batch-arrays.
batch = Transition(*zip(*transitions))
# Compute a mask of non-final states and concatenate the batch elements
# (a final state would've been the one after which simulation ended)
non_final_mask = torch.tensor(tuple(map(lambda s: s is not None, batch.next_state)),
device=device, dtype=torch.bool)
non_final_next_states = torch.cat([s for s in batch.next_state if s is not None])
state_batch = torch.cat(batch.state)
action_batch = torch.cat(batch.action)
reward_batch = torch.cat(batch.reward)
# Compute Q(s_t, a) - the model computes Q(s_t), then we select the
# columns of actions taken. These are the actions which would've been taken
# for each batch state according to policy_net
state_action_values = self.policy_net(state_batch).gather(1, action_batch)
# Compute V(s_{t+1}) for all next states.
# Expected values of actions for non_final_next_states are computed based
# on the "older" target_net; selecting their best reward with max(1)[0].
# This is merged based on the mask, such that we'll have either the expected
# state value or 0 in case the state was final.
next_state_values = torch.zeros(self.batch_size, device=device)
next_state_values[non_final_mask] = self.target_net(non_final_next_states).max(1)[0].detach()
# Compute the expected Q values
expected_state_action_values = (next_state_values * self.gamma) + reward_batch
# Compute Huber loss
loss = F.smooth_l1_loss(state_action_values, expected_state_action_values.unsqueeze(1))
# Optimize the model
self.optimizer.zero_grad()
loss.backward()
for param in self.policy_net.parameters():
param.grad.data.clamp_(-1, 1)
self.optimizer.step()
return loss.item()
We are now reqdy to solve the problem. We need to choose a few hyperparameters: the capacity of the memory replay buffer, the batch size, the learning rate, the discount $\gamma$, the number of episodes, the number of hidden layers and their sizes, and the exploration strategy, that is the starting value for $\epsilon$, the final value, and the decay rate that is applied after each episode. This is typical in reinforcement learning – choose badly and the method will not converge, or will do it much later.
num_observations = env.observation_space.shape[0]
num_actions = env.action_space.n
print(f"Environment has a state of size {num_observations} and {num_actions} actions")
capacity = 10_000
batch_size = 128
agent = DQNAgent(seed=42, num_observations=num_observations, num_actions=num_actions,
hidden_layer_sizes=[128], learning_rate=1e-3, capacity=capacity,
batch_size=batch_size, gamma=0.95)
episodes = 500
epsilon = 0.9
epsilon_min = 0.05
epsilon_decay = 0.99
target_update = 10
losses, episode_rewards, episode_lens, epsilons = [], [], [], []
for i in (pbar := trange(episodes)):
state, done, episode_len, episode_reward = env.reset(), False, 0, 0.0
while not done:
episode_len += 1
action = agent.get_action(state, epsilon)
next_state, reward, done, _ = env.step(action)
agent.remember(state, action, next_state if not done else None, reward)
loss = agent.optimize()
state = next_state
episode_reward += reward
if i % target_update == 0:
agent.sync()
if episode_len > 100:
break
epsilon = max(epsilon_min, epsilon * epsilon_decay)
losses.append(loss / episode_len)
episode_rewards.append(episode_reward)
episode_lens.append(episode_len)
epsilons.append(epsilon)
avg_lens = sum(episode_lens[-50:]) / 50
avg_rewards = sum(episode_rewards[-50:]) / 50
pbar.set_description(f"{max(episode_lens)}/{avg_lens:.2f}/{avg_rewards:.2f}/{epsilon:.2f}")
Environment has a state of size 4 and 2 actions
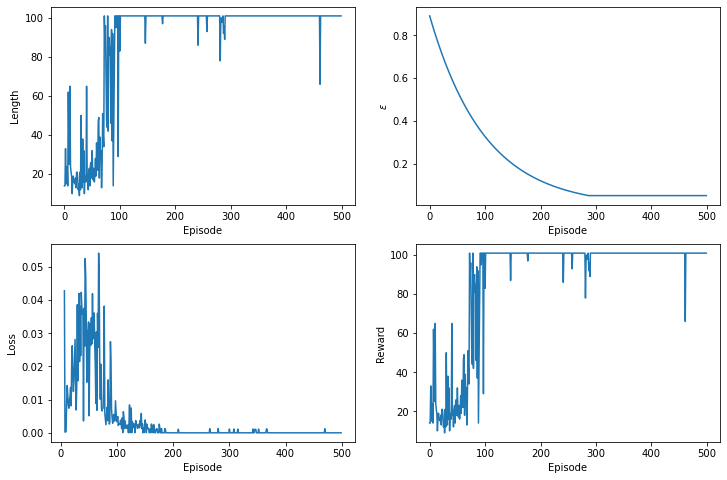
We can visualize the dynamic of the learning phase by plotting the episode length, the $\epsilon$ values, the loss for each optimization, and the total reward accumulated over the episodes.
import matplotlib.pylab as plt
fig, ((ax0, ax1), (ax2, ax3)) = plt.subplots(nrows=2, ncols=2, figsize=(12, 8))
ax0.plot(episode_lens)
ax0.set_xlabel('Episode')
ax0.set_ylabel('Length')
ax1.plot(epsilons)
ax1.set_xlabel('Episode')
ax1.set_ylabel('$\epsilon$')
ax2.plot(losses)
ax2.set_xlabel('Episode')
ax2.set_ylabel('Loss')
ax3.plot(episode_rewards)
ax3.set_xlabel('Episode')
ax3.set_ylabel('Reward');
To test the trained agent, we set $\epsilon=0$ to avoid random actions and always use the optimal strategy.
from PIL import Image, ImageDraw, ImageFont
state = env.reset()
frames, done = [env.render(mode='rgb_array')], False
total_reward = 0.0
while not done:
action = agent.get_action(state, epsilon=0.0)
next_state, reward, done, _ = env.step(action)
total_reward += reward
frame = env.render(mode='rgb_array')
image = Image.fromarray(frame)
draw = ImageDraw.Draw(image)
font = ImageFont.truetype("font3270.otf ", 24)
text = f"Step # {len(frames)}\n"
text += f"action={'left' if action == 0 else 'right'}\n"
text += f"pos={state[0]:.2f}, vel={state[1]:.2f}\nangle={state[2]:.2f}, angle vel={state[3]:.2f}"
draw.multiline_text((10, 10), text, fill=(0, 0, 0), font=font)
state = next_state
frames.append(np.array(image))
print(f"Testing finished after {len(frames)} steps, total reward = {total_reward}")
Testing finished after 201 steps, total reward = 200.0
from matplotlib import pyplot as plt
from matplotlib import animation
# np array with shape (frames, height, width, channels)
video = np.array(frames[:])
fig = plt.figure(figsize=(6, 4))
im = plt.imshow(video[0,:,:,:])
plt.axis('off')
plt.close() # this is required to not display the generated image
def init():
im.set_data(video[0,:,:,:])
def animate(i):
im.set_data(video[i,:,:,:])
return im
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=video.shape[0],
interval=100)
anim.save('./cart-pole-video.mp4')
from IPython.display import Video
Video('./cart-pole-video.mp4')