from abc import ABC, abstractmethod
import matplotlib.pylab as plt
from matplotlib import cm
from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import pandas as pd
import torch
from torch import nn
from scipy.stats import norm
import seaborn as sns
dtype = torch.float32
normal_dist = torch.distributions.Normal(0.0, 1.0)
Model classes.
class Model(ABC):
def __init__(self):
pass
@abstractmethod
def compute_discount_factor(self, t, T):
pass
@abstractmethod
def generate_paths(self, required_schedule, num_paths, dt):
pass
@staticmethod
def generate_schedule(times, dt):
assert len(times) > 0
times = sorted(times)
t_0 = 0.0
schedule = [t_0]
for t in times:
if abs(t - t_0) < 1e-10:
t_0 = t
continue
n = int(np.ceil((t - t_0) / dt)) + 1
schedule += np.linspace(t_0, t, n).tolist()[1:]
t_0 = t
return torch.tensor(list(map(lambda x: round(x, 9), schedule)))
class BlackScholesModel(Model):
def __init__(self, S_0: float, r: float, q: float, σ: float):
self.S_0 = torch.tensor(S_0)
self.r = torch.tensor(r)
self.q = torch.tensor(q)
self.σ = torch.tensor(σ)
def compute_discount_factor(self, t, T):
return np.exp(-self.r * (T - t))
def generate_paths(self, required_schedule, num_paths, dt):
schedule = self.generate_schedule(required_schedule, dt)
self.N = len(schedule)
S_0, r, q, σ = self.S_0, self.r, self.q, self.σ
retval = [torch.full((num_paths,), S_0)]
X = retval[0].log()
W = torch.randn(self.N, num_paths)
t = 0.0
for i in range(0, self.N - 1):
dt = schedule[i + 1] - schedule[i]
t += dt
sqrt_dt = dt.sqrt()
X = X + (r - q - 0.5 * σ**2) * dt + σ * sqrt_dt * W[i, :]
retval.append(X.exp())
return schedule, torch.vstack(retval)
Market classes to buy and sell stock.
class Market(ABC):
@abstractmethod
def cash_flow_shares(self, t, S_t, shares):
"""Buy if positive and sell if negative; result is a negative cash flow for
the former case and a negative cash flow for the latter."""
pass
@abstractmethod
def buy_shares(self, t, S_t, shares):
"Amount of money requires for buying the specified amount of shares."
pass
@abstractmethod
def sell_shares(self, t, S_t, shares):
pass
class NoTransactionCostMarket(Market):
def cash_flow_shares(self, t, S_t, shares):
return -S_t * shares
def buy_shares(self, t, S_t, shares):
assert sum(torch.where(shares < 0.0, torch.tensor(1.0), torch.tensor(0.0))) == 0.0
return S_t * shares
def sell_shares(self, t, S_t, shares):
assert sum(torch.where(shares < 0.0, torch.tensor(1.0), torch.tensor(0.0))) == 0.0
return S_t * shares
class RelativeTransactionCostMarket(Market):
def __init__(self, fraction):
self.fraction = fraction
def cash_flow_shares(self, t, S_t, shares):
multiplier = torch.where(shares > 0, 1 + self.fraction, 1 - self.fraction)
return -multiplier * S_t * shares
def buy_shares(self, t, S_t, shares):
assert sum(torch.where(shares < 0.0, torch.tensor(1.0), torch.tensor(0.0))) == 0.0
return (1 + self.fraction) * S_t * shares
def sell_shares(self, t, S_t, shares):
assert sum(torch.where(shares < 0.0, torch.tensor(1.0), torch.tensor(0.0))) == 0.0
return (1 - self.fraction) * S_t * shares
Contract classes.
class Contract(ABC):
def __init__(self):
pass
@abstractmethod
def description(self):
pass
@abstractmethod
def initialize(self, t, S_t):
pass
@abstractmethod
def advance(self, t, S_t):
pass
@abstractmethod
def execute(self, t, S_t, cash, shares, market: Market):
pass
@abstractmethod
def finalize(self):
pass
@abstractmethod
def black_scholes_price(self, t, S_t, model: BlackScholesModel):
pass
@abstractmethod
def black_scholes_delta(self, t, S_t, model: BlackScholesModel):
pass
@abstractmethod
def required_schedule(self):
pass
@abstractmethod
def monte_carlo_payoffs(self, model: Model, schedule, paths):
pass
@abstractmethod
def num_features():
pass
@abstractmethod
def features(self, model: Model, t, S_t):
pass
class VanillaOption(Contract):
def __init__(self, position, notional: float, K: float, T: float, is_call: float):
assert position in ['L', 'S']
self.position = position
self.long_short = torch.tensor(1.0) if position == 'L' else torch.tensor(-1.0)
self.notional = torch.tensor(notional)
self.K = torch.tensor(K)
self.T = torch.tensor(T)
self.is_call = is_call
def description(self):
long_short = 'long' if self.position == 'L' else 'short'
call_put = 'call' if self.is_call else 'put'
return f'Vanilla {call_put}, {long_short}, K={self.K.item():.4f}, T={self.T.item():.4f}'
def initialize(self, t, S_t):
return torch.zeros_like(S_t), torch.zeros_like(S_t)
def advance(self, t, S_t):
pass
def execute(self, t, S_t, cash, shares, market: Market):
if t != self.T:
# nothing to do before expiry
return cash, shares
if self.position == 'L':
return self._execute_long(t, S_t, cash, shares, market)
else:
return self._execute_short(t, S_t, cash, shares, market)
def finalize(self):
pass
def black_scholes_price(self, t, S_t, model: BlackScholesModel):
notional, T, K = self.notional, self.T, self.K
assert t <= T
r, q, σ = model.r, model.q, model.σ
τ = T - t
F_t = S_t * torch.exp((r - q) * τ)
df = torch.exp(-r * τ)
ω = 1.0 if self.is_call else -1.0
if τ == 0:
return notional * torch.maximum(ω * (S_t - K), torch.tensor(0.0))
d_plus = (torch.log(F_t / K) + 0.5 * σ**2 * τ) / σ / torch.sqrt(τ)
d_minus = d_plus - σ * torch.sqrt(τ)
return self.long_short * notional * ω * df * (F_t * normal_dist.cdf(ω * d_plus) - K * normal_dist.cdf(ω * d_minus))
def black_scholes_delta(self, t, S_t, model: BlackScholesModel):
notional, T, K = self.notional, self.T, self.K
assert t <= T
r, q, σ = model.r, model.q, model.σ
τ = T - t
F_t = S_t * torch.exp((r - q) * τ)
ω = 1.0 if self.is_call else -1.0
if τ == 0:
if self.is_call:
return self.long_short * torch.where(S_t > K, notional, torch.tensor(0.0))
else:
return self.long_short * torch.where(S_t < K, -notional, torch.tensor(0.0))
d_plus = (torch.log(F_t / K) + 0.5 * σ**2 * τ) / σ / torch.sqrt(τ)
return self.long_short * notional * ω * torch.exp(-q * τ) * normal_dist.cdf(ω * d_plus)
def required_schedule(self):
return [self.T]
def monte_carlo_payoffs(self, model, schedule, paths):
S_T = paths[-1]
ω = 1.0 if self.is_call else -1.0
scaling = model.compute_discount_factor(0.0, self.T)
return scaling * self.long_short * self.notional * torch.maximum(ω * (S_T - self.K), torch.tensor(0.0))
def _execute_long(self, t, S_t, cash, shares, market):
if self.is_call:
# the client sell shares if in the money
itm = S_t > self.K
delta_shares = torch.where(itm, self.notional, torch.tensor(0.0))
delta_cash = torch.where(itm, -self.notional, torch.tensor(0.0))
else:
# the client buys shares if in the money
itm = S_t < self.K
# make sure we have the required number of shares
delta_shares = torch.clamp(self.notional - shares, torch.tensor(0.0), self.notional)
delta_shares = torch.where(itm, delta_shares, torch.tensor(0.0))
delta_cash = -market.buy_shares(t, S_t, delta_shares)
# execute transaction
delta_shares -= torch.where(itm, self.notional, torch.tensor(0.0))
delta_cash += torch.where(itm, self.K * self.notional, torch.tensor(0.0))
return cash + delta_cash, shares + delta_shares
def _execute_short(self, t, S_t, cash, shares, market):
if self.is_call:
# the client buys shares if in the money
itm = S_t > self.K
# make sure we have the required number of shares
delta_shares = torch.clamp(self.notional - shares, torch.tensor(0.0), self.notional)
delta_shares = torch.where(itm, delta_shares, torch.tensor(0.0))
delta_cash = -market.buy_shares(t, S_t, delta_shares)
# execute transaction
delta_shares += torch.where(itm, -self.notional, torch.tensor(0.0))
delta_cash += torch.where(itm, self.K * self.notional, torch.tensor(0.0))
else:
# the client seels the shares if in the money
itm = S_t < self.K
delta_shares = torch.where(itm, self.notional, torch.tensor(0.0))
delta_cash = torch.where(itm, -self.notional * self.K, torch.tensor(0.0))
return cash + delta_cash, shares + delta_shares
def num_features(self):
return 2
def features(self, model: Model, t, S_t):
return [torch.full(S_t.shape, t).unsqueeze(-1),
(S_t / model.S_0).log().unsqueeze(-1)]
class BlackScholesAnalyticPricer:
def __init__(self, model: BlackScholesModel):
self.model = model
def price(self, contract, t, S_t):
return contract.black_scholes_price(t, S_t, self.model)
def delta(self, contract, t, S_t):
return contract.black_scholes_delta(t, S_t, self.model)
class BlackScholesMonteCarloPricer:
def __init__(self, model: BlackScholesModel):
self.model = model
def price(self, contract, schedule, paths):
payoffs = contract.monte_carlo_payoffs(self.model, schedule, paths)
return payoffs.mean(), payoffs.std() / torch.sqrt(torch.tensor(float(len(payoffs))))
market = NoTransactionCostMarket()
model = BlackScholesModel(100.0, 0.05, 0.02, 0.25)
analytic_pricer = BlackScholesAnalyticPricer(model)
mc_pricer = BlackScholesMonteCarloPricer(model)
We verify that analytic and Monte Carlo prices agree.
short_vanilla_call = VanillaOption('S', 1.0, 95.0, 0.5, True)
long_vanilla_call = VanillaOption('L', 1.0, 95.0, 0.5, True)
for contract in [short_vanilla_call, long_vanilla_call]:
print(contract.description() + ':')
torch.manual_seed(42)
contract.initialize(0.0, model.S_0)
analytic_price = analytic_pricer.price(contract, 0.0, model.S_0)
print(f"Analytic price: {analytic_price:.4f}", end='')
schedule, paths = model.generate_paths(contract.required_schedule(), 10_000, 1.0 / 52)
mc_price, mc_std = mc_pricer.price(contract, schedule, paths)
CI = (mc_price - 1.96 * mc_std, mc_price + 1.96 * mc_std)
print(f', Monte Carlo price: [{CI[0]:.4f}, {CI[1]:.4f}]', end='')
if analytic_price < CI[0] or analytic_price > CI[1]:
print(' -> *ERROR*')
else:
print(' -> OK')
print()
Vanilla call, short, K=95.0000, T=0.5000:
Analytic price: -10.3924, Monte Carlo price: [-10.6495, -10.1216] -> OK
Vanilla call, long, K=95.0000, T=0.5000:
Analytic price: 10.3924, Monte Carlo price: [10.1216, 10.6495] -> OK
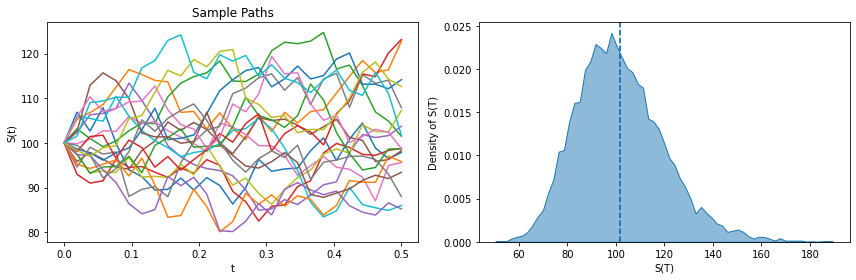
fig, (ax0, ax1) = plt.subplots(ncols=2, figsize=(12, 4))
for i in range(20):
ax0.plot(schedule, paths[:, i])
ax0.set_xlabel('t')
ax0.set_ylabel('S(t)')
ax0.set_title('Sample Paths')
sns.histplot(paths[-1], ax=ax1, element='poly', stat='density', alpha=0.5)
ax1.axvline(x=paths[-1].mean(), linestyle='dashed')
ax1.axvline(model.S_0 * torch.exp((model.r - model.q) * contract.T), linestyle='dashed')
ax1.set_xlabel('S(T)')
ax1.set_ylabel('Density of S(T)')
fig.tight_layout()
class Hedger(ABC):
@abstractmethod
def description(self):
pass
@abstractmethod
def calibrate(self, **kwargs):
pass
@abstractmethod
def hedge(self, t, S_t, shares):
pass
class BlackScholesHedger(Hedger):
def __init__(self, model: BlackScholesModel, contract: Contract):
self.contract = contract
self.pricer = BlackScholesAnalyticPricer(model)
def description(self):
return 'Black-Scholes hedger'
def calibrate(self, **kwargs):
pass
def hedge(self, t, S_t, shares):
return -self.pricer.delta(self.contract, t, S_t)
class HedgeNet(nn.Module):
def __init__(self, num_features):
super().__init__()
self.layers = nn.Sequential(
nn.Linear(num_features, 64),
nn.ReLU(),
nn.Linear(64, 32),
nn.ReLU(),
nn.Linear(32, 16),
nn.ReLU(),
nn.Linear(16, 1)
)
def forward(self, x):
return self.layers(x)
class DeepHedger(Hedger):
def __init__(self, model, contract: Contract, market, scaling_price):
self.model = model
self.contract = contract
self.market = market
self.scaling_price = scaling_price
def description(self):
return 'Deep Hedger'
def calibrate(self, **kwargs):
batch_size = kwargs['batch_size']
lr = kwargs['lr']
num_iters = kwargs['num_iters']
num_paths = kwargs['num_paths']
max_dt = kwargs['max_dt']
print_every = kwargs['print_every']
net = HedgeNet(contract.num_features())
optimizer = torch.optim.Adam(net.parameters(), lr=lr)
for i in range(num_iters):
total_loss = 0.0
schedule, paths = self.model.generate_paths(contract.required_schedule(), num_paths, max_dt)
diff_schedule = torch.from_numpy(np.diff(schedule))
batches = torch.split(paths, batch_size, dim=1)
for batch in batches:
cash, shares = contract.initialize(schedule[0], batch[0])
for t, dt, S_t in zip(schedule[:-1], diff_schedule, batch[:-1]):
contract.advance(t, S_t)
x = torch.hstack(contract.features(self.model, t, S_t))
delta = net(x).squeeze(1)
cash += market.cash_flow_shares(t, S_t, delta - shares)
shares = delta
# interest on cash
cash *= torch.exp(self.model.r * dt)
# cash coming from the dividends
cash += shares * S_t * (torch.exp(self.model.q * dt) - 1)
assert cash.shape == batch[0].shape
assert shares.shape == batch[0].shape
T, S_T = schedule[-1], batch[-1]
cash, shares = contract.execute(T, S_T, cash, shares, market)
contract.finalize()
# liquidate all remaining positions
cash += market.cash_flow_shares(T, S_T, -shares)
# discount to model date
cash *= torch.exp(-self.model.r * T)
# minimize square error
loss = cash.var() / (self.scaling_price**2)
total_loss += loss.item()
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss /= len(batches)
if (i + 1) % print_every == 0:
print(f"Iter {i + 1:4}: loss = {total_loss:.4e}")
self.net = net
def hedge(self, t, S_t, shares):
x = torch.hstack(contract.features(self.model, t, S_t))
y = self.net(x).squeeze(1).detach()
return y
contract = VanillaOption('S', 1.0, 105.0, 0.25, True)
bs_model = BlackScholesModel(S_0=100.0, r=0.05, q=0.02, σ=0.25)
analytic_pricer = BlackScholesAnalyticPricer(bs_model)
bs_price = analytic_pricer.price(contract, 0.0, bs_model.S_0)
print(f"Black-Scholes price: {bs_price.item():.4f}")
Black-Scholes price: -3.2393
bs_hedger = BlackScholesHedger(bs_model, contract)
deep_hedger = DeepHedger(bs_model, contract, NoTransactionCostMarket(), bs_price)
torch.manual_seed(42)
deep_hedger.calibrate(batch_size=32, lr=0.5e-3, num_iters=100, num_paths=1_000, max_dt=1 / 256,
scaling_price=bs_price, print_every=10)
Iter 10: loss = 1.4471e-01
Iter 20: loss = 8.1138e-02
Iter 30: loss = 6.7405e-02
Iter 40: loss = 5.0502e-02
Iter 50: loss = 5.0674e-02
Iter 60: loss = 4.0541e-02
Iter 70: loss = 3.5466e-02
Iter 80: loss = 3.6956e-02
Iter 90: loss = 3.9783e-02
Iter 100: loss = 3.3974e-02
class Agent(ABC):
@abstractmethod
def execute(self, contract: Contract, market: Market, hedger: Hedger):
pass
class BlackScholesAgent(Agent):
def __init__(self, model: BlackScholesModel, frequency: float, num_paths: int):
self.model = model
self.frequency = frequency
self.num_paths = num_paths
def execute(self, contract: Contract, market: Market, hedger: Hedger, seed):
torch.manual_seed(seed)
schedule, paths = self.model.generate_paths(contract.required_schedule(), self.num_paths, self.frequency)
diff_schedule = torch.from_numpy(np.diff(schedule))
cash, shares = contract.initialize(schedule[0], paths[0])
for t, dt, S_t in zip(schedule[:-1], diff_schedule, paths[:-1]):
contract.advance(t, S_t)
new_shares = hedger.hedge(t, S_t, shares)
cash += market.cash_flow_shares(t, S_t, new_shares - shares)
shares = new_shares
# interest on cash
cash *= torch.exp(self.model.r * dt)
# cash coming from the dividends
cash += shares * S_t * (torch.exp(self.model.q * dt) - 1)
assert cash.shape == paths[0].shape
assert shares.shape == paths[0].shape
T, S_T = schedule[-1], paths[-1]
cash, shares = contract.execute(T, S_T, cash, shares, market)
contract.finalize()
# liquidate all remaining positions
cash += market.cash_flow_shares(T, S_T, -shares)
# discount to model date
cash *= torch.exp(-self.model.r * T)
hedger_price = cash.mean()
hedger_std = cash.std() / np.sqrt(self.num_paths)
# for debugging
self.schedule = schedule
self.paths = paths
return hedger_price, hedger_std, cash
agent = BlackScholesAgent(model, frequency=1 / 256, num_paths=1_000)
market = NoTransactionCostMarket()
results = {}
for hedger in[bs_hedger, deep_hedger]:
hedger_price, hedger_std, cash = agent.execute(contract, market, hedger, seed=42)
print(f"Hedger price = {hedger_price:.4f}, std = {hedger_std:.4f}, Black-Scholes price: {bs_price:.4f}, "\
f"diff = {hedger_price - bs_price:.4f}")
print(f"Hedger std dev / price = {cash.std() / bs_price:.4f}")
results[hedger.description()] = cash
Hedger price = -3.2524, std = 0.0169, Black-Scholes price: -3.2393, diff = -0.0131
Hedger std dev / price = -0.1647
Hedger price = -3.2620, std = 0.0197, Black-Scholes price: -3.2393, diff = -0.0226
Hedger std dev / price = -0.1927
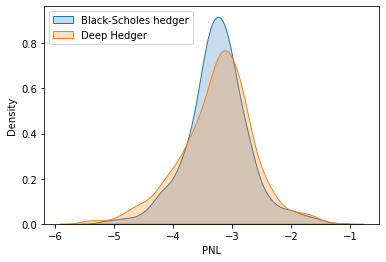
for k, v in results.items():
sns.kdeplot(v, label=k, shade=True)
plt.legend(loc='upper left')
plt.xlabel('PNL')
plt.ylabel('Density');
bs_deltas, deep_deltas = [], []
timegrid = torch.linspace(0.0, contract.T * 0.9, 100)
spots = torch.linspace(model.S_0 * 0.9, model.S_0 * 1.1, 100)
contract.initialize(0.0, spots)
for t in timegrid:
bs_deltas.append(bs_hedger.hedge(t, spots, 0.0).tolist())
deep_deltas.append(deep_hedger.hedge(t, spots, 0.0).tolist())
bs_deltas = np.array(bs_deltas)
deep_deltas = np.array(deep_deltas)
import matplotlib.pylab as plt
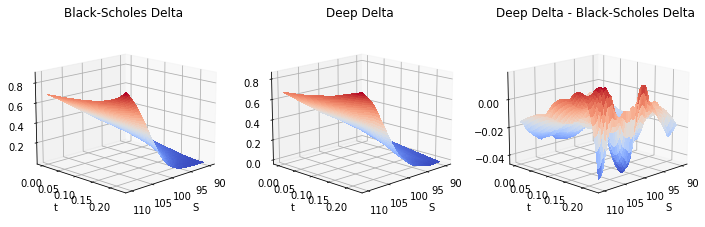
fig, (ax0, ax1, ax2) = plt.subplots(subplot_kw={'projection': '3d'}, ncols=3, figsize=(12, 4))
X, Y = np.meshgrid(spots, timegrid)
ax0.plot_surface(X, Y, bs_deltas, cmap=cm.coolwarm, linewidth=0, antialiased=False)
ax0.set_title('Black-Scholes Delta')
ax1.plot_surface(X, Y, deep_deltas, cmap=cm.coolwarm, linewidth=0, antialiased=False)
ax1.set_title('Deep Delta')
ax2.plot_surface(X, Y, deep_deltas - bs_deltas, cmap=cm.coolwarm, linewidth=0, antialiased=False)
ax2.set_title('Deep Delta - Black-Scholes Delta')
for ax in [ax0, ax1, ax2]:
ax.set_xlabel('S')
ax.set_ylabel('t')
ax.view_init(15, 45)