Another interesting code exercise is the eight queens problem, well-known to chess players and first proposed in 1848. The problem on the classical $8 \times 8$ chessboard can be generalized on a $n \times n$ one; the number of solutions are known. It is easy to code a function that finds one solution; here we want to find them all.
The Python environment is quite simple and only requires standard packages.
$ python -mv venv venv
$ ./venv/Scripts/activate
$ pip install numpy numba matplotlib
import copy
from matplotlib.colors import LinearSegmentedColormap
import matplotlib.pylab as plt
from numba import njit
import numpy as np
colors = ['white', 'dimgrey']
n_bins = [0, 1, 2, 100]
cmap = LinearSegmentedColormap.from_list('chessboard', colors, N=2)
Focusing on the $8 \times 8$ case, the first step is to visualize a combination on the chessboard to inspect the validity of a solution. We do it using matplotlib: for each queen, we put a circle on each square that is attacked by that queen; the color of the circle is green if there is no queen on it or red otherwise. The function get_threats() returns the (i, j) coordinates that a queen in $(i_{queen}, j_{queen})$ attacks on a $n \times $n chessboard.
@njit
def get_threats(i_queen, j_queen, n):
retval = set()
for i in range(n):
if i != i_queen:
retval.add((i, j_queen))
for j in range(n):
if j != j_queen:
retval.add((i_queen, j))
for d in range(-n, n):
i, j = d + i_queen, d + j_queen
if i >= 0 and i < n and j >= 0 and j < n and i != i_queen and j != j_queen:
retval.add((i, j))
i, j = d + i_queen, -d + j_queen
if i >= 0 and i < n and j >= 0 and j < n and i != i_queen and j != j_queen:
retval.add((i, j))
return retval
def plot_board(board):
plt.figure(figsize=(6, 6))
n, m = board.shape
assert n == m
assert n == 8, 'plot_board() is tailored for n=8'
base = np.zeros((n, n), dtype=np.int8)
for i in range(n):
for j in range(n):
base[i, j] = (i + j * n) % 2 == (j % 2)
plt.imshow(base, cmap=cmap)
queens = []
threats = set()
for i in range(n):
for j in range(n):
if board[i, j] == 1:
queens.append((i, j))
threats = threats.union(get_threats(i, j, n))
for i, j in threats:
color = 'salmon' if board[i, j] == 1 else 'lightgreen'
circle = plt.Circle((i, j), 0.35, fc=color, ec=color, alpha=0.8)
plt.gca().add_patch(circle)
for i, j in queens:
plt.text(i, j, '♕', horizontalalignment='center', verticalalignment='center', fontsize=28)
plt.axis('off')
We test plot_board() with two cases, one where the two queens attack each other and another in which they don’t. We can see the red circles in the first case and all green circles in the second, as expected.
board = np.zeros((8, 8), dtype=np.int8)
board[2, 2] = 1
board[5, 5] = 1
plot_board(board)
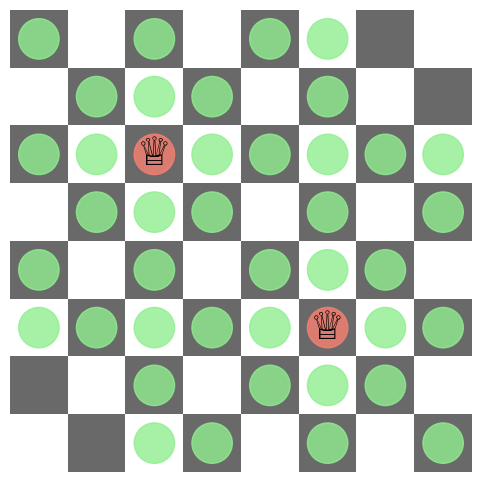
board = np.zeros((8, 8), dtype=np.int8)
board[0, 1] = 1
board[7, 6] = 1
plot_board(board)

And now the code of the algorithm: function add_queen() tries to add a queen in the coordinates i_queen, j_queen. If that square is already menaced by the other queens, the function returns no solutions, otherwise it inserts the queen. If by doing so we have inserted n queens, we have a solution and we return that, otherwise we continue by adding a new queen. Since we know that no two queens can be on the same row, we can go to the next row directly when trying for new queens.
def add_queen(board, i_queen, j_queen, other_queens, n):
# (i_queen, j_queen) are the coordinates of the queen we want to insert,
# so we check first if this can be done
# are we menaced by the queens already on the chessboard?
for other_queen in other_queens:
if (i_queen, j_queen) in get_threats(*other_queen, n):
return []
# we can add the new queen, return the solution
board[i_queen, j_queen] = 1.0
# if we have all the eight queens, we are done
if len(other_queens) == n - 1:
retval = copy.deepcopy(board)
# remove the queen before returning
board[i_queen, j_queen] = 0.0
return [retval]
solutions = []
for i in range(0, n):
# a new queen on the same column will not work, skip
if i == i_queen:
continue
# look at the next row
new_solutions = add_queen(board, i, len(other_queens) + 1, other_queens + [(i_queen, j_queen)], n)
if len(new_solutions) > 0:
solutions += new_solutions
# return the queen before returning
board[i_queen, j_queen] = 0.0
return solutions
def find_solutions(n):
board = np.zeros((n, n), dtype=np.int8)
solutions = []
for i in range(n):
solutions += add_queen(board, i, 0, [], n)
# check we have no repeated solutions
assert len(set((s.tobytes() for s in solutions))) == len(solutions)
return solutions
As it is easy to see, he cases $n=2$ and $n=3$ have no solutions. For $n=4$ there are two solutions.
solutions = find_solutions(4)
print(f"Found {len(solutions)} solutions.")
Found 2 solutions.
For the chessboard case, $n=8$, that there are $\binom{64}{8} = 4,426,165,368$ possibly combinations, of which only 92 are solutions. However, since we must have one queen per row, the number of combinations is reduced to $8^8 = 16,777,216$, which is still large but much more manageable. (For the $n=12$ case, though, the “reduced” number of combinations would be $12^12 = 8,916,100,448,256$, which is surely not small.)
solutions = find_solutions(8)
print(f"Found {len(solutions)} solutions.")
Found 92 solutions.
plot_board(solutions[0])
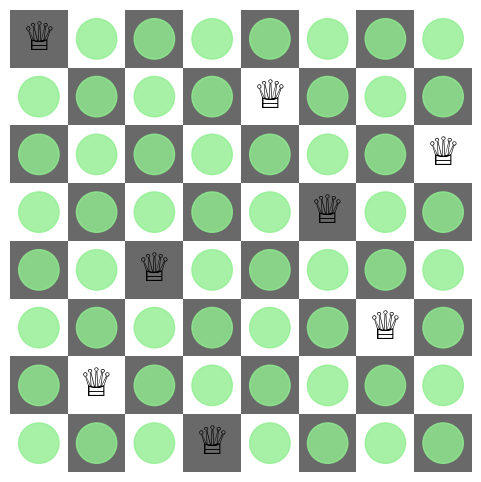
solutions = find_solutions(9)
print(f"Found {len(solutions)} solutions.")
Found 352 solutions.
solutions = find_solutions(10)
print(f"Found {len(solutions)} solutions.")
Found 724 solutions.
solutions = find_solutions(11)
print(f"Found {len(solutions)} solutions.")
Found 2680 solutions.
solutions = find_solutions(12)
print(f"Found {len(solutions)} solutions.")
Found 14200 solutions.
This solves our exercise. A much shorter and elegant, but a bit more cryptic, solution can be found on the wikipedia web page using coroutines. The data structures are simpler (one queen per row, going from the first two to the last), which then makes it easier to find the squares under attach. Using yield makes the code extremely concise and should be remembered for the next recursive algorithm
def queens(n, i, a, b, c):
if i < n:
for j in range(n):
if j not in a and i+j not in b and i-j not in c:
yield from queens(n, i+1, a+[j], b+[i+j], c+[i-j])
else:
yield a
for solution in queens(8, 0, [], [], []):
print(solution)
[0, 4, 7, 5, 2, 6, 1, 3]
[0, 5, 7, 2, 6, 3, 1, 4]
[0, 6, 3, 5, 7, 1, 4, 2]
[0, 6, 4, 7, 1, 3, 5, 2]
[1, 3, 5, 7, 2, 0, 6, 4]
[1, 4, 6, 0, 2, 7, 5, 3]
[1, 4, 6, 3, 0, 7, 5, 2]
[1, 5, 0, 6, 3, 7, 2, 4]
[1, 5, 7, 2, 0, 3, 6, 4]
[1, 6, 2, 5, 7, 4, 0, 3]
[1, 6, 4, 7, 0, 3, 5, 2]
[1, 7, 5, 0, 2, 4, 6, 3]
[2, 0, 6, 4, 7, 1, 3, 5]
[2, 4, 1, 7, 0, 6, 3, 5]
[2, 4, 1, 7, 5, 3, 6, 0]
[2, 4, 6, 0, 3, 1, 7, 5]
[2, 4, 7, 3, 0, 6, 1, 5]
[2, 5, 1, 4, 7, 0, 6, 3]
[2, 5, 1, 6, 0, 3, 7, 4]
[2, 5, 1, 6, 4, 0, 7, 3]
[2, 5, 3, 0, 7, 4, 6, 1]
[2, 5, 3, 1, 7, 4, 6, 0]
[2, 5, 7, 0, 3, 6, 4, 1]
[2, 5, 7, 0, 4, 6, 1, 3]
[2, 5, 7, 1, 3, 0, 6, 4]
[2, 6, 1, 7, 4, 0, 3, 5]
[2, 6, 1, 7, 5, 3, 0, 4]
[2, 7, 3, 6, 0, 5, 1, 4]
[3, 0, 4, 7, 1, 6, 2, 5]
[3, 0, 4, 7, 5, 2, 6, 1]
[3, 1, 4, 7, 5, 0, 2, 6]
[3, 1, 6, 2, 5, 7, 0, 4]
[3, 1, 6, 2, 5, 7, 4, 0]
[3, 1, 6, 4, 0, 7, 5, 2]
[3, 1, 7, 4, 6, 0, 2, 5]
[3, 1, 7, 5, 0, 2, 4, 6]
[3, 5, 0, 4, 1, 7, 2, 6]
[3, 5, 7, 1, 6, 0, 2, 4]
[3, 5, 7, 2, 0, 6, 4, 1]
[3, 6, 0, 7, 4, 1, 5, 2]
[3, 6, 2, 7, 1, 4, 0, 5]
[3, 6, 4, 1, 5, 0, 2, 7]
[3, 6, 4, 2, 0, 5, 7, 1]
[3, 7, 0, 2, 5, 1, 6, 4]
[3, 7, 0, 4, 6, 1, 5, 2]
[3, 7, 4, 2, 0, 6, 1, 5]
[4, 0, 3, 5, 7, 1, 6, 2]
[4, 0, 7, 3, 1, 6, 2, 5]
[4, 0, 7, 5, 2, 6, 1, 3]
[4, 1, 3, 5, 7, 2, 0, 6]
[4, 1, 3, 6, 2, 7, 5, 0]
[4, 1, 5, 0, 6, 3, 7, 2]
[4, 1, 7, 0, 3, 6, 2, 5]
[4, 2, 0, 5, 7, 1, 3, 6]
[4, 2, 0, 6, 1, 7, 5, 3]
[4, 2, 7, 3, 6, 0, 5, 1]
[4, 6, 0, 2, 7, 5, 3, 1]
[4, 6, 0, 3, 1, 7, 5, 2]
[4, 6, 1, 3, 7, 0, 2, 5]
[4, 6, 1, 5, 2, 0, 3, 7]
[4, 6, 1, 5, 2, 0, 7, 3]
[4, 6, 3, 0, 2, 7, 5, 1]
[4, 7, 3, 0, 2, 5, 1, 6]
[4, 7, 3, 0, 6, 1, 5, 2]
[5, 0, 4, 1, 7, 2, 6, 3]
[5, 1, 6, 0, 2, 4, 7, 3]
[5, 1, 6, 0, 3, 7, 4, 2]
[5, 2, 0, 6, 4, 7, 1, 3]
[5, 2, 0, 7, 3, 1, 6, 4]
[5, 2, 0, 7, 4, 1, 3, 6]
[5, 2, 4, 6, 0, 3, 1, 7]
[5, 2, 4, 7, 0, 3, 1, 6]
[5, 2, 6, 1, 3, 7, 0, 4]
[5, 2, 6, 1, 7, 4, 0, 3]
[5, 2, 6, 3, 0, 7, 1, 4]
[5, 3, 0, 4, 7, 1, 6, 2]
[5, 3, 1, 7, 4, 6, 0, 2]
[5, 3, 6, 0, 2, 4, 1, 7]
[5, 3, 6, 0, 7, 1, 4, 2]
[5, 7, 1, 3, 0, 6, 4, 2]
[6, 0, 2, 7, 5, 3, 1, 4]
[6, 1, 3, 0, 7, 4, 2, 5]
[6, 1, 5, 2, 0, 3, 7, 4]
[6, 2, 0, 5, 7, 4, 1, 3]
[6, 2, 7, 1, 4, 0, 5, 3]
[6, 3, 1, 4, 7, 0, 2, 5]
[6, 3, 1, 7, 5, 0, 2, 4]
[6, 4, 2, 0, 5, 7, 1, 3]
[7, 1, 3, 0, 6, 4, 2, 5]
[7, 1, 4, 2, 0, 6, 3, 5]
[7, 2, 0, 5, 1, 4, 6, 3]
[7, 3, 0, 2, 5, 1, 6, 4]