Here we explore tabular reinforcement learning, and Q-learning in particular, without using any packages or classes. This only works for simple tabular methods, and it is a good step to do to learn the basic steps and methods of reinforcement learning. The goal of this code is to explore every single implementation detail; once this is done, the OpenAI Gym environments are the fast bet. Tabular methods have limited utility and rarely work, so in the future we will focus on more advanced methods.
The environment we want to solve is a maze, defined as a Cartesian grid of positions containing a |, + and + to indicate a wall where the agent cannot go and a space to indicate a position that can be filled by the agent. The initial position is shown with I (in). The agent has to move to reach the O (out) position, at which he has reached his goal.
The maze is defined as a string. The agent cannot exit the grid or otherwise fall out – if he is close to the border, his actions will be limited such that he remains on the grid. We assume we have one starting position and one final position, and all transictions and actions are deterministic.
import copy
import numpy as np
import pandas as pd
import random
from typing import Any, Tuple, List
from abc import ABC, abstractmethod
from matplotlib.pylab import plt
%matplotlib inline
The fist class we define is the Space class.
class Space(ABC):
"""Generic definition of space. It supports continuous and discrete spaces in arbitrary dimensions.
The elements of the space are tuples."""
@abstractmethod
def num_dimensions(self) -> int:
pass
@abstractmethod
def random_element(self) -> Tuple[Any]:
pass
class DiscreteSpace(Space):
"""A space with only one dimension and a finite number of elements. Each element of the space has an associated rank,
whic is a number between 0 and n - 1, where n is the number of elements in the space. The element order is not important."""
def num_dimensions(self) -> int:
return 1
@abstractmethod
def size(self) -> int:
"""Returns the size of the space, that is the number of elements contains into it."""
pass
@abstractmethod
def rank(self, element: Tuple[Any]) -> int:
"Returns a rank from 0 to size - 1 for the given element."
pass
@abstractmethod
def is_valid(self, element: Tuple[Any]) -> bool:
"Returns True if the element is a valid element of the space or False otherwise"
pass
@abstractmethod
def element(self, rank: int) -> Tuple[Any]:
"Returns the element corresponding to the given rank."
pass
@abstractmethod
def all_elements(self) -> List[Any]:
pass
class DoubleIdentityDiscreteSpace(DiscreteSpace):
"""A trivial implementation to be used when the elements are already the range from 0 to n-1.
In this case we know that the rank of element i is i itself, and vice-versa."""
def __init__(self, nx: int, ny: int):
assert nx > 0 and ny > 0, "input parameters 'nx' and 'ny' must be positive"
self.nx = nx
self.ny = ny
self.n = nx * ny
def size(self) -> int:
return self.n
def random_element(self) -> Tuple[Any]:
"We select a random element with uniform probability."
rank = np.random.choice(self.n)
return self.element(rank)
def rank(self, element: Tuple[Any]) -> int:
assert self.is_valid(element), "invalid input element"
i, j = element
return i + (j - 1) * self.nx
def is_valid(self, element: Tuple[Any]) -> bool:
i, j, = element
assert isinstance(i, int) and isinstance(j, int), "input element i and j must be an integer"
if i < 0 or i >= self.nx:
return False
if j < 0 or j >= self.ny:
return False
return True
def element(self, rank: int) -> Tuple[Any]:
i = rank % self.nx
j = rank // self.ny
return (i, j)
def all_elements(self) -> List[Any]:
retval = []
for rank in range(self.size()):
retval.append(self.element(rank))
return retval
class DictDiscreteSpace(DiscreteSpace):
"""Implementation of the DiscreteSpace class that uses dictionaries to move from elements to ranks and viceversa."""
def __init__(self, elements):
self.elements = elements
self.element_to_rank = {}
self.rank_to_element = {}
for rank, element in enumerate(elements):
self.element_to_rank[element] = rank
self.rank_to_element[rank] = element
self.n = len(elements)
def size(self) -> int:
return self.n
def random_element(self) -> Tuple[Any]:
"We select a random element with uniform probability."
random_rank = np.random.choice(self.n)
random_element = self.element(random_rank)
return random_element
def rank(self, element: Tuple[Any]) -> int:
e, = element
return self.element_to_rank[e]
def is_valid(self, element: Tuple[Any]) -> bool:
e, = element
return e in self.elements
def element(self, rank: int) -> Tuple[Any]:
return self.rank_to_element[rank],
def all_elements(self) -> List[Any]:
retval = []
for rank in range(self.size()):
retval.append(self.element(rank))
return retval
class Environment(ABC):
@abstractmethod
def state_space(self) -> Space:
"""Returns the state space."""
pass
@abstractmethod
def action_space(self) -> Space:
"""Returns the action space."""
pass
@abstractmethod
def initialize(self) -> None:
"""Initializes the environment; to be called before each episode."""
pass
@abstractmethod
def initial_state(self) -> Tuple[Any]:
"""Returns the rank of the initial state."""
pass
@abstractmethod
def step(self, state: Tuple[Any], action: Tuple[Any]) -> (Tuple[Any], float, bool, Any):
"""For the given current state and action, it returns the new state, the reward and a boolean
that is True if the next state is final or zero otherwise, as well as a generic info object that can be used
for debugging."""
pass
class LearningRate(ABC):
"""Class that defines the learning rate, also called $\alpha$ in the literature."""
@abstractmethod
def initialize(self, state_space: DiscreteSpace, action_space: DiscreteSpace) -> None:
"""Initializes the object for the given state and action spaces."""
pass
@abstractmethod
def __call__(self, time_step: int, state_rank: int, action_rank: int) -> float:
"""Returns the learning rate for the given episode, state and action ranks."""
pass
class ConstantLearningRate(LearningRate):
"A constant learning rate."
def __init__(self, alpha):
self.alpha = alpha
def initialize(self, state_space: Space, action_space: Space) -> None:
pass
def __call__(self, time_step: int, state_rank: int, action_rank: int) -> float:
return self.alpha
class OneOverTimeStepLearningRate(LearningRate):
"Learning rate defined as one over the episode."
def __init__(self, omega: float = 1.0):
assert omega > 0.5 and omega <= 1
self.omega = omega
def initialize(self, state_space: Space, action_space: Space) -> None:
pass
def __call__(self, time_step: int, state_rank: int, action_rank: int) -> float:
return 1.0 / (time_step**self.omega)
class OneOverVisitsLearningRate(LearningRate):
"Learning rate $\alpha defined as 1 over the number of times the state/action pair has been visited, plus one."
def initialize(self, state_space: Space, action_space: Space) -> None:
num_states = state_space.size()
num_actions = action_space.size()
self.visits = np.zeros((num_states, num_actions))
def __call__(self, time_step: int, state_rank: int, action_rank: int) -> float:
self.visits[state_rank, action_rank] += 1
return 1.0 / (self.visits[state_rank, action_rank])
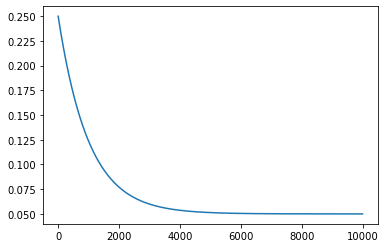
It is typical to use the so-called $\epsilon-$greedy strategy to add some randomness to the algorithm. Given an number $\epsilon \in (0, 1)$, we choose with probability $1-\epsilon$ what currently is the best strategy, and with probability $\epsilon$ we select a random action. By selecting the current best strategy we exploit the policy we currently have; with the random action instead we explore different, and possibly untested, actions. It is paramount to find the good balance between exploration (of uncharted territory) and exploitation (of current knowledge). For that, it is often convenient to use $\epsilon = \epsilon(t)$. At the beginning, the exploration rate is at its highest value, because we don’t know anything much about the environment, so we need to do a lot of exploration by randomly choosing our actions. As the environment is explored, $\epsilon$ gets small, reflecting increased confidence in the estimated Q values.
class ExplorationRate(ABC):
"""Class defining the exploration rate, also called $\epsilon$ in the literature.
An exploration rate of 1 means that we explore 100% of times; an exploration rate of 0% means we never explore."""
@abstractmethod
def __call__(self, episode: int) -> float:
"""Returns the epsilon value for the given episode"""
pass
class ConstantExplorationRate(ExplorationRate):
"A constant value."
def __init__(self, epsilon: float):
assert epsilon > 0.0 and epsilon <= 1.0, "bad epsilon value"
self.epsilon = epsilon
def __call__(self, episode: int) -> float:
return self.epsilon
class ExponentiallyDecayingExplorationRate(ExplorationRate):
"""Exponentially decaying. The initial value is decayed after each episode and floored to a minimum value."""
def __init__(self, max_epsilon: float, min_epsilon: float, decay_rate: float):
assert max_epsilon >= min_epsilon, "input parameter 'max_epsilon' cannot be less than 'min_epsilon'"
assert min_epsilon >= 0, "input parameter 'min_epsilon' cannot be negative"
assert decay_rate >= 0.0, "input parameter 'decay_rate' cannot be negative"
self.min_epsilon = min_epsilon
self.max_epsilon = max_epsilon
self.decay_rate = decay_rate
def __call__(self, episode: int) -> float:
assert episode >= 0
return self.min_epsilon + (self.max_epsilon - self.min_epsilon) * np.exp(-self.decay_rate * episode)
class PureExplorationRate(ExplorationRate):
def __call__(self, episode: int) -> float:
return 1.0
time_steps = range(1, 10000)
exp_epsilon = ExponentiallyDecayingExplorationRate(0.25, 0.05, 1.0 / 1000)
plt.plot(time_steps, list(map(exp_epsilon, time_steps)))
[<matplotlib.lines.Line2D at 0x189d95025b0>]
class ReinforcementLearning(ABC):
"""Abstract interface for all reinforcement learning methods."""
@abstractmethod
def set_environment(self, env: Environment) -> None:
"""Initializes the object with the given environment, learning rate and exploration rate."""
pass
@abstractmethod
def train(self, num_episodes: int, discount: float, params=None) -> None:
"""Trains the model using the specified number of episodes and learning rate."""
pass
@abstractmethod
def optimal_action(self, state: Tuple[Any]) -> Tuple[Any]:
"""Returns the action defined by the optimal policy for the specified state."""
pass
@staticmethod
def get_param(params, key, default_value):
if params is None or key not in params:
return default_value
return params[key]
class Observer(ABC):
@abstractmethod
def observe(self, episode: int, time: int, alpha: float, state: Tuple[Any], action: Tuple[Any], reward: float, is_final: bool, Q) -> None:
pass
class RewardsObserver(Observer):
def __init__(self):
self.rewards = {}
def observe(self, episode: int, time: int, alpha: float, state: Tuple[Any], action: Tuple[Any], reward: float, is_final: bool, Q) -> None:
# in this simplified version we only care about the final step
if episode not in self.rewards:
self.rewards[episode] = []
self.rewards[episode].append(reward)
Tabular-based RL methods.
class TabularReinforcementLearning(ReinforcementLearning):
"""Base class for all tabular-based reinforcement learning methods."""
@abstractmethod
def set_learning_rate(self, learning_rate: LearningRate) -> None:
pass
@abstractmethod
def set_exploration_rate(self, exploration_rate: ExplorationRate) -> None:
pass
@abstractmethod
def set_observer(self, observer) -> None:
pass
@abstractmethod
def optimal_action_rank(self, state_rank: int) -> int:
"""Returns the action rank defined by the optimal policy for the specified state rank."""
pass
We focus on Temporal Difference (TD) methods, of which the most important are SARSA and Q Learning. Since SARSA and Q Learning are very similar, we adopt a semi-virtual class that defines the initial Q matrix in the initialize() method and also implements the optimal_action() method.
class MatrixBasedReinforcementLearning(TabularReinforcementLearning):
"""Semi-abstract class that provides common constructor, initialize() method and optimal_action() to Q Learning and SARSA.
It describes the learning methods that require the matrix Q explicitly.
Utility functions are provided as well."""
def __init__(self):
pass
def set_environment(self, env: Environment) -> None:
self.env = env
assert isinstance(env.state_space(), DiscreteSpace), "a discrete state space is needed"
self.num_states = env.state_space().size()
assert isinstance(env.action_space(), DiscreteSpace), "a discrete action space is needed"
self.num_actions = env.action_space().size()
def set_learning_rate(self, learning_rate: LearningRate) -> None:
self.learning_rate = learning_rate
def set_exploration_rate(self, exploration_rate: ExplorationRate) -> None:
self.exploration_rate = exploration_rate
def set_observer(self, observer) -> None:
self.observer = observer
def initialize(self) -> None:
# define a zero Q matrix
self.Q = np.zeros((self.num_states, self.num_actions))
print("We have {} states and {} actions".format(self.num_states, self.num_actions))
# keep track of the number of visits
self.N = np.zeros((self.num_states, self.num_actions))
# for debugging
self.num_explorations = 0
self.num_exploitations = 0
self.epsilons = []
def choose_epsilon(self, time_step: int, state_rank: int) -> float:
eps = self.exploration_rate(time_step)
self.epsilons.append(eps)
return eps
def nanmax(self, values) -> float:
# FIXME -- to be removed
# max value discarding nans
return values[~np.isnan(values)].max()
def argmax(self, values) -> float:
# position of max values
max_value = self.nanmax(values)
for i, item in enumerate(values):
if np.isnan(item): continue
if item == max_value:
return i
raise ValueError("Cannot find maximum")
def select_action(self, epsilon: float, state_rank: int) -> int:
do_exploration = np.random.binomial(1, epsilon) == 1
values = self.Q[state_rank]
if do_exploration:
# with probability epsilon, explore randomly among all choices (all equally probable)
valid_action_ranks = []
for i in range(self.num_actions):
if values[i] > -np.inf:
valid_action_ranks.append(i)
assert len(valid_action_ranks) > 0, "no valid actions!"
action = np.random.choice(valid_action_ranks)
self.num_explorations += 1
else:
# with probability 1 - epsilon, choose the best action. If many actions are the best ones,
# choose randomly amongst those
max_value = self.nanmax(values)
best_action_ranks = []
for i in range(self.num_actions):
if values[i] == max_value:
best_action_ranks.append(i)
action = random.choice(best_action_ranks)
self.num_exploitations += 1
return action
def optimal_action_rank(self, state_rank: int) -> int:
return self.argmax(self.Q[state_rank])
def optimal_action(self, state: Tuple[Any]) -> Tuple[Any]:
state_rank = self.env.state_space().rank(state)
action_rank = self.optimal_action_rank(state_rank)
return self.env.action_space().element(action_rank)
def print_stats(self):
total = self.num_exploitations + self.num_explorations
print("")
print("Exploitation = {:.2f}%, exploration = {:.2f}%".format(100 * self.num_exploitations / total, 100 * self.num_explorations / total))
class QLearning(MatrixBasedReinforcementLearning):
def __init__(self):
pass
def train(self, num_episodes: int, discount: float, params=None) -> None:
max_steps_per_episode = QLearning.get_param(params, 'MaxStepsPerEpisode', 1e6)
print_frequency = QLearning.get_param(params, 'PrintFrequency', 1000)
# initialize the learning rate object
self.learning_rate.initialize(self.env.state_space(), self.env.action_space())
time = 1
# loop over all the episodes
for episode in range(num_episodes):
total_reward = 0.0
self.env.initialize()
state = self.env.initial_state()
state_rank = self.env.state_space().rank(state)
episode_time = 0
# continue till when the episode has reached the end or we have exhausted the allotted time
while True:
epsilon = self.choose_epsilon(episode, state)
# select the action to perform amongst the possible one, with an epsilon-greedy strategy
action_rank = self.select_action(epsilon, state_rank)
action = self.env.action_space().element(action_rank)
# find the next state corresponding to the action selected
next_state, reward, is_final, _ = self.env.step(state, action)
if is_final:
Q_max = 0.0
else:
next_state_rank = self.env.state_space().rank(next_state)
Q_max = self.nanmax(self.Q[next_state_rank])
new_estimate = reward + discount * Q_max
alpha = self.learning_rate(time, state_rank, action_rank)
self.Q[state_rank, action_rank] = (1 - alpha) * self.Q[state_rank, action_rank] + alpha * new_estimate
self.N[state_rank, action_rank] += 1
#
self.observer.observe(episode, episode_time, alpha, state, action, reward, is_final, self.Q)
# total (undiscounted) reward for this episode
total_reward += reward
time += 1
# if final we stop
if is_final:
break
# go to next state unless we have been living too long
if episode_time > max_steps_per_episode:
raise ValueError("episode {} did not finish in {} steps".format(episode, time))
# reset the state for the next iteration
state_rank = next_state_rank
state = next_state
if episode > 0 and episode % print_frequency == 0 and print_frequency != -1:
print("step {} finished".format(episode))
self.print_stats()
class SARSA(MatrixBasedReinforcementLearning):
def __init__(self):
pass
def train(self, num_episodes: int, discount: float, learning_rate: LearningRate, params=None):
max_steps_per_episode = 1e6 if params is None else params['MaxStepsPerEpisode']
# initialize the learning rate object
learning_rate.initialize(self.env.state_space(), self.env.action_space())
retval = ConvergenceInfo()
# global counter of steps
time_step = 0
# loop over all the episodes
for episode in range(num_episodes):
total_reward = 0.0
env.initialize()
state_rank = env.initial_state()
episode_time_step = 0
# first action
epsilon = self.choose_epsilon(episode, state_rank)
# select the action to perform amongst the possible one, with an epsilon-greedy strategy
action_rank = self.select_action(epsilon, state_rank)
# continue till when the episode has reached the end or we have exhausted the allotted time
num_steps = 0
while True:
# find the next state corresponding to the action selected
next_state_rank, reward, is_final = self.env.step(state_rank, action_rank)
# find the best action for the next state
next_epsilon = self.choose_epsilon(episode, next_state_rank)
next_action_rank = self.select_action(next_epsilon, next_state_rank)
# update part
row_mean = self.nanmean(self.Q[next_state_rank])
row_max = self.nanmax(self.Q[next_state_rank])
delta = reward + discount * (epsilon * row_mean + (1 - epsilon) * row_max) - self.Q[state_rank, action_rank]
self.Q[state_rank, action_rank] += self.learning_rate(episode, state_rank, action_rank) * delta
self.N[state_rank, action_rank] += 1
total_reward += reward
if is_final:
retval.append(total_reward, num_steps)
break
# go to next state
time_step += 1
episode_time_step += 1
if episode_time_step > max_steps_per_episode:
raise ValueError("episode {} did not finish in {} steps".format(episode, max_steps_per_episode))
# reset the state for the next iteration
state_rank = next_state_rank
action_rank = next_action_rank
epsilon = next_epsilon
if episode > 0 and episode % 500 == 0:
print("step {} finished".format(episode))
self.print_stats(retval)
return retval
def nanmean(self, values) -> float:
# max value discarding nans
return values[~np.isnan(values)].mean()
This final class is for visualization and debugging. It provides an abstract interface to paint an environment.
class Visualization(ABC):
@abstractmethod
def initialize(self):
"Initializes the visualization to the a blank state."
pass
@abstractmethod
def write(self, state: Tuple[Any], content: Any) -> None:
"Writes the given content at the specified state."
pass
@abstractmethod
def finalize(self):
"Finalizes the visualization and paints to the screen."
pass
Sample problems, from quite small, to medium, to relatively large. The data has been generated from http://www.delorie.com/game-room/mazes/genmaze.cgi, with the added initial and final positions.
# a trival example (3x3)
data1 = """
+--+--+--+
I |
+ +--+--+
| |
+--+--+ +
| O
+--+--+--+
"""
# a slightly bigger one (10x10)
data2 = """
+--+--+--+--+--+--+--+--+--+--+
I | | |
+ +--+--+ + +--+ + +--+--+
| | | | | |
+ + +--+--+--+ +--+--+--+ +
| | | | | | |
+--+--+ + + + + + + + +
| | | | | | |
+ +--+--+ + +--+--+--+--+ +
| | | | | |
+ + + + +--+--+--+ +--+ +
| | | | | |
+ +--+ + + + +--+--+ +--+
| | | | | |
+ +--+--+--+ +--+--+--+--+ +
| | | | | |
+--+ + + +--+--+ + + + +
| | | | | | | | |
+ +--+ + +--+ + + + + +
| | | | O
+--+--+--+--+--+--+--+--+--+--+
"""
# a challenging one (20x20)
data3 = """
+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+
I | | | | |
+--+ + + +--+ +--+--+ + +--+ +--+--+--+--+--+--+--+ +
| | | | | | | | | |
+ +--+ +--+ + + + +--+--+ +--+--+--+--+--+ + + + +
| | | | | | | | | |
+ + + + + + +--+--+ +--+--+ + +--+ + +--+--+--+ +
| | | | | | | | | | | | |
+--+--+--+ + +--+ +--+--+--+ +--+ + +--+--+ + +--+--+
| | | | | | | | | | |
+ + + +--+--+--+ + + +--+--+ + + + + + +--+--+ +
| | | | | | | | | | |
+ +--+--+ +--+ +--+ +--+--+ +--+--+--+--+--+--+--+--+--+
| | | | | | | | |
+ +--+--+--+ + +--+--+ +--+--+ +--+--+ + +--+--+ + +
| | | | | | | | | | | | | |
+ + +--+ + + + + +--+--+ + + + + + +--+ + + +
| | | | | | | | | | | |
+ +--+ +--+--+ + +--+--+ +--+ +--+--+--+--+--+--+ + +
| | | | | | | | | | | | |
+ + +--+--+--+--+ + + + + + + + + +--+ + + + +
| | | | | | | | | | | | | |
+ +--+--+ + + +--+ + + +--+ +--+ + + +--+ +--+--+
| | | | | | | | | | | | |
+--+--+--+--+ + + + + +--+--+--+--+ + + + + +--+ +
| | | | | | | | | | | |
+ + +--+ + +--+--+--+--+ + + + +--+ + + + + +--+
| | | | | | | | | | | | |
+--+--+ +--+ + +--+ + +--+--+ + +--+--+--+--+--+ + +
| | | | | | | | |
+ +--+--+ +--+--+ +--+ +--+--+--+--+ + + +--+ +--+ +
| | | | | | | | | | |
+ +--+ +--+ + +--+--+--+ + + +--+--+ + + +--+ + +
| | | | | | | | | | | |
+ + + + + +--+--+ +--+--+--+--+ + + +--+--+--+--+--+
| | | | | | | | | | | | |
+ + + + + + + + + +--+--+--+ + +--+--+--+ + + +
| | | | | | | | | | | |
+ +--+ +--+--+ + +--+--+--+--+ + +--+--+--+--+ +--+ +
| | | | O
+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+--+
"""
# which problem we want to solve
data = data2
class MazeEnvironment(Environment):
"""
Wrapper of the world grid.
A state is a two-element tuple with the current row and the column entry.
An action is a character giving the direction, which is one of north, east, south and west.
"""
NORTH = 'N'
SOUTH = 'S'
EAST = 'E'
WEST = 'W'
INITIAL = 'I'
FINAL = 'O'
WALLS = ['+', '|', '-']
HOLE = 'H'
EMPTY = ' '
def __init__(self, data):
self.world = self._build_world(data)
self.num_rows = self.world.shape[0]
self.num_cols = self.world.shape[1]
self.states = DoubleIdentityDiscreteSpace(nx=self.num_rows, ny=self.num_cols)
# all possible actions
all_actions = [self.NORTH, self.EAST, self.SOUTH, self.WEST]
self.actions = DictDiscreteSpace(all_actions)
self._initial_state = self._get_initial_state()
def state_space(self) -> Space:
return self.states
def action_space(self) -> Space:
return self.actions
def initialize(self) -> None:
pass
def initial_state(self) -> int:
return self._initial_state
def is_final_state(self, state_rank) -> bool:
state = self.states.element(state_rank)
cell = self.world[state]
return cell in [FINAL, HOLE]
def step(self, state: Tuple[Any], action_tuple: Tuple[Any]) -> (int, float, bool, None):
row, col = state
cell = self.world[row, col]
action, = action_tuple
assert cell in [self.EMPTY, self.INITIAL], "bad input state" + cell
# get the location on the grid
if action == self.WEST:
new_state = (row, col - 1)
if action == self.EAST:
new_state = (row, col + 1)
if action == self.NORTH:
new_state = (row - 1, col)
if action == self.SOUTH:
new_state = (row + 1, col)
# all invalid actions bring the agent back to the initial position, with a hefty negative reward
if new_state[0] < 0 or new_state[0] >= self.world.shape[0] or new_state[1] < 0 or new_state[1] >= self.world.shape[1]:
new_state = state
reward = -np.inf
is_final = True
else:
new_cell = self.world[new_state]
if new_cell in self.WALLS:
new_state = None
reward = -np.inf
is_final = True
elif new_cell == self.FINAL:
reward = 0
is_final = True
elif new_cell == self.HOLE:
reward = -100.0
is_final = True
else:
reward = -1
is_final = False
return new_state, reward, is_final, None
def new_world(self):
return copy.deepcopy(self.world)
def _build_world(self, data):
"""Given the input as a strings, it builds the matrix with the world description.
The world is a matrix, with each entry defined as (row, column). The top left element
is (0, 0), the top right (0, num_cols-1), and so on.
Going north means moving one row up (so decreasing the row counter), moving east
means moving one more column.
"""
assert len([k for k in data if k == self.INITIAL]) == 1, "no initial position found or more than one"
assert len([k for k in data if k == self.FINAL]) > 0, "no final position found"
world = []
for row in data.split('\n'):
if len(row) == 0: continue
world.append([x for x in row])
lengths = map(len, world)
if len(set(lengths)) != 1:
raise ValueError("world must be a rectangular matrix")
return np.array(world)
def _get_initial_state(self):
for i in range(self.num_rows):
for j in range(self.num_cols):
entry = self.world[i, j]
if entry == self.INITIAL:
return (i, j)
def visualize(self, matrix) -> None:
pass
class MazeVisualization(Visualization):
def __init__(self, env: MazeEnvironment, algorithm: ReinforcementLearning):
self.env = env
self.algorithm = algorithm
def initialize(self):
self.world = env.new_world()
# mark the object as initialized
self.initialized = True
def write(self, state : Any, content : Any) -> None:
assert self.initialized, "object has not been initialized"
self.world[state] = content
def finalize(self):
return '\n'.join(map(lambda x: ''.join(x), self.world))
def optimal_policy(self):
self.initialize()
counter = 0
MAX_STEPS = 1000
state = self.env.initial_state()
total_steps = 1
while True:
action = self.algorithm.optimal_action(state)
new_state, _, is_final, _ = self.env.step(state, action)
total_steps += 1
self.write(state, '*')
if is_final or counter > MAX_STEPS:
break
state = new_state
counter += 1
#
print("Total number of steps = {}".format(total_steps))
return self.finalize()
env = MazeEnvironment(data)
algorithm = QLearning()
algorithm.set_environment(env)
algorithm.set_learning_rate(ConstantLearningRate(0.25))
algorithm.set_exploration_rate(ConstantExplorationRate(0.25))
algorithm.set_observer(RewardsObserver())
algorithm.initialize()
algorithm.train(10_000, discount=1, params={'PrintFrequency': 2000})
We have 651 states and 4 actions
step 2000 finished
step 4000 finished
step 6000 finished
step 8000 finished
Exploitation = 75.03%, exploration = 24.97%
viz = MazeVisualization(env, algorithm)
print(viz.optimal_policy())
Total number of steps = 113
+--+--+--+--+--+--+--+--+--+--+
*********** | | |
+ +--+--+* + +--+ + +--+--+
| | ****** | | | |
+ + *+--+--+--+ +--+--+--+ +
| | *** |*****| | | |
+--+--+* +* + *+ + + + + +
| ****** |* | *| | | |
+ *+--+--+* + *+--+--+--+--+ +
| *|*****|* | ********* | |
+ *+* + *+* +--+--+--+* +--+ +
| *** | *|* | ********* | |
+ +--+ *+* + *+ +--+--+ +--+
| | *** | *| | |
+ +--+--+--+ *+--+--+--+--+ +
| | | *******|*****| |
+--+ + + +--+--+ *+* + *+ +
| | | | | *|* | *| |
+ +--+ + +--+ + *+* + *+ +
| | | *** | ****O
+--+--+--+--+--+--+--+--+--+--+