A very interesting application of reinforcement learning was presented in this 2013 article, followed in 2015 by another publication on Nature, available for download on the DeepMind website.
What we want to do in this post is to solve the MsPacman-v0 environement using the classical deep Q-Learning algorithm. MsPacman-v0 is one of the Atari 2600 games, and it uses the atari_py package to connect to the Atari emulator. The onservation is the RGB image of the screen, which is an array of size $(210, 160, 3)$. There are at least two versions in Gym: MsPacman-v0, which has as observsation the image as we said, and MsPacman-ram-v0, which returns the 128 bytes of the RAM.
The game is well known and simple to play and understand: the agent plays Ms. PacMan in a maze. There are dots; the goal is to each all the dots. A level is finished when all the dots are eaten. There are also four ghots who try to catch Ms. PacMan; if this happens a life is lost. Four power-up items are found in the corners of the maze, called power pills, which are worth 40 points each. When Ms. PacMan consumes a power-pill all ghosts become edible, i.e. the ghosts turn blue for a short period (15 seconds), they slow down and try to escape from Ms. PacMan. During this time, Ms. PacMan is able to eat them, which is worth 200, 400, 800 and 1600 points, consecutively. The ghosts move following a deterministic strategy, with some randomness added such that there is no simple optimal decision process. The observation space is discrete yet fairly large – more than a thousand positions in the maze, plus the position of the agent, the ghosts, the power pills; besides, the ghosts can be eatable or not.
The code is largely inspired for what is proposed in the book Reinforcemente Learning Hands-On. Let’s start with some imports:
import cv2
import gym
import gym.spaces
import matplotlib.pylab as plt
import numpy as np
import collections
import time
The approach we follow is similar to the one presented in the 2013 paper: images are resized to $84 \times 84$ pixels, and several images are condensed together to generate a state. This is done using Gym wrappers, of which we have a few. The first one takes care of taking a certain number of frames to skip. During these frames the agent repeats the same action, while the observations are stored and glued together using a max operation on arrays.
class MaxAndSkipEnv(gym.Wrapper):
def __init__(self, env, skip):
super().__init__(env)
self._obs_buffer = collections.deque(maxlen=skip)
self._skip = skip
def step(self, action):
total_reward = 0.0
done = None
for _ in range(self._skip):
obs, reward, done, info = self.env.step(action)
self._obs_buffer.append(obs)
total_reward += reward
if done:
break
max_frame = np.max(np.stack(self._obs_buffer), axis=0)
return max_frame, total_reward, done, info
def reset(self):
self._obs_buffer.clear()
obs = self.env.reset()
self._obs_buffer.append(obs)
return obs
The ProcessFrame84 wrapper resizes the frame to a smaller image. This is done to reduce the computational complexity; the number 84 comes from the paper. The three color layers are dropped and a single gray image is used instead.
class ProcessFrame84(gym.ObservationWrapper):
def __init__(self, env=None):
super().__init__(env)
self.observation_space = gym.spaces.Box(low=0, high=255, shape=(84, 84, 1), dtype=np.uint8)
def observation(self, obs):
return ProcessFrame84.process(obs)
@staticmethod
def process(frame):
assert frame.size == 210 * 160 * 3
img = np.reshape(frame, [210, 160, 3]).astype(np.float32)
# convert to a single color
img = img[:, :, 0] * 0.229 + img[:, :, 1] * 0.587 + img[:, :, 2] * 0.114
# reduce the image resolution
resized_screen = cv2.resize(img, (84, 84), interpolation=cv2.INTER_AREA)
x_t = np.reshape(resized_screen, [84, 84, 1])
return x_t.astype(np.uint8)
The BufferWrapper is used to extend the observations from images to a mini-video. The idea is that a single image doesn’t convey what is needed to play the video game: speed and direction of movement. Using n_steps observations can hopefully do that. Following the 2013 paper, we use n_steps=4; a larger number would improve the performances by increase the computational cost.
class BufferWrapper(gym.ObservationWrapper):
def __init__(self, env, n_steps, dtype=np.float32):
super().__init__(env)
self.dtype = dtype
old_space = env.observation_space
self.observation_space = gym.spaces.Box(
old_space.low.repeat(n_steps, axis=0),
old_space.high.repeat(n_steps, axis=0), dtype=dtype)
def reset(self):
self.buffer = np.zeros_like(self.observation_space.low, dtype=self.dtype)
return self.observation(self.env.reset())
def observation(self, observation):
self.buffer[:-1] = self.buffer[1:]
self.buffer[-1] = observation
return self.buffer
Finally, we need to convert the image to the PyTorch format and scale the values to be in the $[0, 1]$ range.
class ImageToPyTorch(gym.ObservationWrapper):
def __init__(self, env):
super().__init__(env)
old_shape = self.observation_space.shape
new_shape = (old_shape[-1], old_shape[0], old_shape[1])
self.observation_space = gym.spaces.Box(
low=0.0, high=1.0, shape=new_shape, dtype=np.float32)
def observation(self, observation):
return np.moveaxis(observation, 2, 0)
class ScaledFloatFrame(gym.ObservationWrapper):
def observation(self, obs):
return np.array(obs).astype(np.float32) / 255.0
We put together all the wrappers. The frameskip variable is set to one because we take care of this ourselves; also, we use a smaller action space. The meaning of the actions are NOOP, UP, RIGHT, LEFT, DOWN, UPRIGHT, UPLEFT, DOWNRIGHT,
DOWNLEFT and can be obtained using gym.make('MsPacman-v0').get_action_meanings().
def make_env(env_name):
env = gym.make(env_name, frameskip=1, full_action_space=False)
env = MaxAndSkipEnv(env, skip=16)
env = ProcessFrame84(env)
env = ImageToPyTorch(env)
env = BufferWrapper(env, n_steps=4)
return ScaledFloatFrame(env)
We are ready for the interesting part: creating the Deep Q-Learning model.
import torch
import torch.nn as nn
class DQN(nn.Module):
def __init__(self, input_shape, n_actions):
super().__init__()
self.conv = nn.Sequential(
nn.Conv2d(input_shape[0], 32, kernel_size=8, stride=4),
nn.ReLU(),
nn.Conv2d(32, 64, kernel_size=4, stride=2),
nn.ReLU(),
nn.Conv2d(64, 64, kernel_size=3, stride=2),
nn.ReLU())
conv_out_size = self._get_conv_out(input_shape)
self.fc = nn.Sequential(
nn.Linear(conv_out_size, 512),
nn.ReLU(),
nn.Linear(512, n_actions))
def _get_conv_out(self, shape):
o = self.conv(torch.zeros(1, *shape))
return int(np.prod(o.size()))
def forward(self, x):
conv_out = self.conv(x).view(x.size()[0], -1)
return self.fc(conv_out)
import torch.optim as optim
ENV_NAME = 'MsPacman-v0'
As we said above, an observation in our case is more of short video, composed of only four frames. One single frame (that is, a static image) wouldn’t suffice to describe the movement and the speed at which the little ghosts chase our agent. Using more than four frames would help, but also slow the training. What we do in the cell below is to use a random agent and perform one hundred steps (each of which is indeed composed by four steps), then visualize the state in four different images.
env = make_env(ENV_NAME)
env.reset()
for _ in range(100):
observation, reward, _, _ = env.step(env.action_space.sample())
fig, axes = plt.subplots(figsize=(12, 4), ncols=4)
for i in range(4):
axes[i].imshow(observation[i])
axes[i].set_axis('off')
axes[i].set_title(f'Frame #{i}')
env.close()
del env
As suggested in the paper, it is important to use the experience replay buffer. An entry in the
experience replay buffer is implemented in Python using a namedtuple with five fields that map the current state, the action, the reward,
a boolean to mark final states, and the new state.
Experience = collections.namedtuple('Experience',
field_names=['state', 'action', 'reward', 'done', 'new_state'])
The ExperienceBuffer class is quite simple: we want to keep the last capacity entries, and
we do this using a deque. The sample() method selects a few entry randomly (to reduce the correlation
among the samples) and wraps them in NumPy arrays.
class ExperienceBuffer:
def __init__(self, capacity):
self.buffer = collections.deque(maxlen=capacity)
def __len__(self):
return len(self.buffer)
def append(self, experience):
self.buffer.append(experience)
def sample(self, batch_size):
indices = np.random.choice(len(self.buffer), batch_size, replace=False)
states, actions, rewards, dones, next_states = zip(*[self.buffer[idx] for idx in indices])
return np.array(states), np.array(actions), \
np.array(rewards, dtype=np.float32), np.array(dones, dtype=np.uint8), \
np.array(next_states)
The Agent class encapsulates the logic of the agent.
class Agent:
def __init__(self, env, exp_buffer):
self.env = env
self.exp_buffer = exp_buffer
self._reset()
def _reset(self):
self.state = self.env.reset()
self.total_reward = 0.0
@torch.no_grad()
def play_step(self, net, epsilon=0.0, device):
done_reward = None
if np.random.random() < epsilon:
action = self.env.action_space.sample()
else:
state_a = np.array([self.state], copy=False)
state_v = torch.tensor(state_a).to(device)
q_vals_v = net(state_v)
_, act_v = torch.max(q_vals_v, dim=1)
action = int(act_v.item())
new_state, reward, is_done, _ = self.env.step(action)
self.total_reward += reward
exp = Experience(self.state, action, reward, is_done, new_state)
self.exp_buffer.append(exp)
self.state = new_state
if is_done:
done_reward = self.total_reward
self._reset()
return done_reward
def calc_loss(batch, net, tgt_net, device):
states, actions, rewards, dones, next_states = batch
states_v = torch.tensor(np.array(states, copy=False)).to(device)
next_states_v = torch.tensor(np.array(next_states, copy=False)).to(device)
actions_v = torch.tensor(actions, dtype=torch.int64).to(device)
rewards_v = torch.tensor(rewards).to(device)
done_mask = torch.BoolTensor(dones).to(device)
state_action_values = net(states_v).gather(1, actions_v.unsqueeze(-1)).squeeze(-1)
with torch.no_grad():
next_state_values = tgt_net(next_states_v).max(1)[0]
next_state_values[done_mask] = 0.0
next_state_values = next_state_values.detach()
expected_state_action_values = next_state_values * GAMMA + rewards_v
return nn.MSELoss()(state_action_values, expected_state_action_values)
We are now ready to start the training.
GAMMA = 0.99
BATCH_SIZE = 128
REPLAY_SIZE = 10_000
REPLAY_START_SIZE = 10_000
LEARNING_RATE = 1e-4
SYNC_TARGET_FRAMES = 1_000
EPSILON_DECAY_LAST_FRAME = 250_000
EPSILON_START = 1.0
EPSILON_FINAL = 0.01
MAX_ITERATIONS = 2_000_000
device = "cuda" # or use "cpu" if not available
env = make_env(ENV_NAME)
net = DQN(env.observation_space.shape, env.action_space.n).to(device)
tgt_net = DQN(env.observation_space.shape, env.action_space.n).to(device)
buffer = ExperienceBuffer(REPLAY_SIZE)
agent = Agent(env, buffer)
epsilon = EPSILON_START
optimizer = optim.Adam(net.parameters(), lr=LEARNING_RATE)
total_rewards = []
frame_idx = 0
ts_frame = 0
ts = time.time()
best_m_reward = None
history = []
%%time
while frame_idx < MAX_ITERATIONS:
frame_idx += 1
epsilon = max(EPSILON_FINAL, EPSILON_START - frame_idx / EPSILON_DECAY_LAST_FRAME)
reward = agent.play_step(net, epsilon, device=device)
if reward is not None:
total_rewards.append(reward)
speed = (frame_idx - ts_frame) / (time.time() - ts)
ts_frame = frame_idx
ts = time.time()
m_reward = np.mean(total_rewards[-100:])
#print(f"{frame_idx:,}: done {len(total_rewards)} games, reward {m_reward:.3f}, "
# f"eps {epsilon:.2f}, speed {speed:.2f} f/s")
history.append((frame_idx, m_reward, epsilon, speed))
if best_m_reward is None or best_m_reward < m_reward:
torch.save(net.state_dict(), ENV_NAME + ".dat")
if best_m_reward is not None:
print(f"{frame_idx}: best reward updated {best_m_reward:.3f} -> {m_reward:.3f} (eps: {epsilon:.2}, speed: {speed:.2f} f/s)")
best_m_reward = m_reward
if len(buffer) < REPLAY_START_SIZE:
continue
if frame_idx % SYNC_TARGET_FRAMES == 0:
tgt_net.load_state_dict(net.state_dict())
optimizer.zero_grad()
batch = buffer.sample(BATCH_SIZE)
loss_t = calc_loss(batch, net, tgt_net, device=device)
loss_t.backward()
optimizer.step()
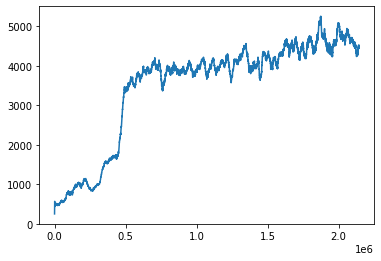
By plotting the history we can see the progress of the agent, which goes from a few hundreds to just above fie thousands.
history_array = np.array(history)
plt.plot(history_array[:, 0], history_array[:, 1])
[<matplotlib.lines.Line2D at 0x18c1dba6f10>]
After training it is time to see the model in action.
FPS = 5
env = make_env(ENV_NAME)
net = DQN(env.observation_space.shape, env.action_space.n)
state = torch.load(ENV_NAME + ".dat", map_location=lambda stg, _: stg)
net.load_state_dict(state)
observation = env.reset()
total_reward = 0.0
c = collections.Counter()
frames = [env.render(mode='rgb_array')]
done = False
while not done:
start_ts = time.time()
frames.append(env.render(mode='rgb_array'))
observation_v = torch.tensor(np.array([observation], copy=False))
q_vals = net(observation_v).data.numpy()[0]
action = np.argmax(q_vals)
c[action] += 1
observation, reward, done, _ = env.step(action)
total_reward += reward
if done:
break
delta = 1 / FPS - (time.time() - start_ts)
if delta > 0:
time.sleep(delta)
env.close()
frames = frames[1:]
from matplotlib import pyplot as plt
from matplotlib import animation
# np array with shape (frames, height, width, channels)
video = np.array(frames[:])
fig = plt.figure(figsize=(8, 10))
im = plt.imshow(video[0,:,:,:])
plt.axis('off')
plt.close() # this is required to not display the generated image
def init():
im.set_data(video[0,:,:,:])
def animate(i):
im.set_data(video[i,:,:,:])
return im
anim = animation.FuncAnimation(fig, animate, init_func=init, frames=video.shape[0],
interval=100)
anim.save('./MsPacman-video.mp4')
from IPython.display import Video
Video('./MsPacman-video.mp4')