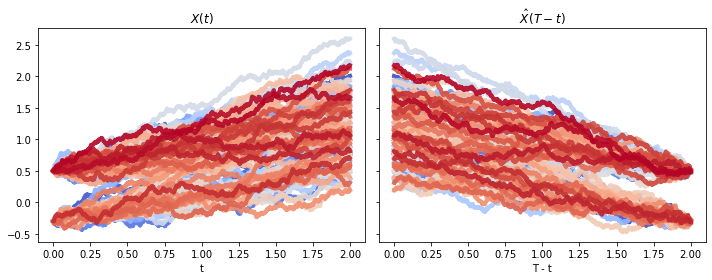
The score-based generative modeling method is based on a result on stochastic differential equation that was published in a 1982 paper by Brian D.O. Anderson. What we will do here is to present the result and provide an implementation for a simple case with analytical solution.
import numpy as np
from matplotlib.pyplot import cm
import matplotlib.pylab as plt
import seaborn as sns
T = 2.0
n = 1001
t_all = np.linspace(0, T, n)
Δt_all = np.diff(t_all)
sqrt_Δt_all = np.sqrt(Δt_all)
μ = 0.5
σ = 0.25
regime_probs = [0.4, 0.6]
X_0_values = [-0.3, 0.5]
num_regimes = len(regime_probs)
def compute_forward_process():
regime = np.random.choice(range(num_regimes), p=regime_probs)
X_0 = X_0_values[regime]
retval = [X_0]
X = retval[0]
for i in range(n - 1):
Δt = Δt_all[i]
sqrt_Δt = sqrt_Δt_all[i]
Z = np.random.randn()
X += μ * Δt + σ * sqrt_Δt * Z
retval.append(X)
return retval
def compute_backward_process(X_T):
retval = [X_T]
X = X_T
for i in range(n - 1, 0, -1):
t = t_all[i]
Δt = Δt_all[i - 1]
sqrt_Δt = sqrt_Δt_all[i - 1]
Z = np.random.randn()
p, grad = 0.0, 0.0
σ2t = σ**2 * t
for regime in range(num_regimes):
ω = regime_probs[regime]
X_0 = X_0_values[regime]
e = np.exp(-0.5 * (X - X_0 - μ * t)**2 / σ2t)
p += ω * e
grad += -ω * (X - X_0 - μ * t) / σ2t * e
grad_log_p = -grad / p
X += (-μ - σ**2 * grad_log_p) * Δt + σ * sqrt_Δt * Z
retval.append(X)
return retval
num_paths = 100
forward_paths = [compute_forward_process() for _ in range(num_paths)]
backward_paths = [compute_backward_process(f[-1]) for f in forward_paths]
fig, (ax0, ax1) = plt.subplots(figsize=(10, 4), ncols=2, sharey=True)
for ax in (ax0, ax1):
ax.set_prop_cycle('color',[cm.coolwarm(i) for i in np.linspace(0, 1, num_paths)])
for path in forward_paths:
ax0.plot(t_all, path, linewidth=4, alpha=0.9)
for path in backward_paths:
ax1.plot(t_all, path, linewidth=4, alpha=0.9)
ax0.set_xlabel('t')
ax0.set_title('$X(t)$')
ax1.set_xlabel('T - t')
ax1.set_title('$\hat X(T - t)$')
fig.tight_layout()