Description

The title of my PhD Thesis in Applied Mathematics is Domain Decomposition Preconditioners: Theoretical Properties, Application to the Compressible Euler Equations, Parallel Aspects. The advisor is Prof. A. Quarteroni. The thesis was obtained at the Ecole Polytechnique Federale de Lausanne (EPFL), and part of the financing was given by the IDeMAS project. The thesis can be downloaded from the EPFL library.

Abstract

The purpose of this thesis is to define efficient parallel preconditioners based on the domain decomposition paradigm and to apply them to the solution of the steady compressible Euler equations.

In the first part we propose and analyse various domain decomposition preconditioners of both overlapping (Schwarz) and non-overlapping (Schur complement-based) type. For the former, we deal with two-level methods, with an algebraic formulation of the coarse space. This approach enjoys several interesting properties not always shared by more standard two-level methods. For the latter, we introduce a class of preconditioners based on a peculiar decomposition of the computational domain. The domain is decomposed in such a way that one subdomain is connected to all the others, which are in fact disconnected components. A class of approximate Schur complement preconditioners is also considered. Theoretical and numerical results are given for a model problem.

In the second part we consider the application of the previous domain decomposition preconditioners to the compressible Euler equations. The discretisation procedure, based on multidimensional upwind residual distribution schemes, is outlined. We introduce a framework that combines non-linear system solvers, Krylov accelerators, domain decomposition preconditioners, as well as mesh adaptivity procedures. Several numerical tests of aeronautical interest are carried out in order to assess both the discretisation schemes and the mesh adaptivity procedures.

In the third part we consider the parallel aspects inherent in the numerical solution of the compressible Euler equations on parallel computers with distributed memory. All the main kernels of the solution algorithm are analysed. Many numerical tests are carried out, with the aim of investigating the performance of the domain decomposition preconditioners proposed in the first part of the thesis, in the applications addressed in the second part.

Visualization

A couple of nice images, made with Visual3. The data were obtained using the code THOR (developed during the IDeMAS project and my PhD thesis). The following figure provides an illustration of the results of an Euler calculation around a complete Falcon aircraft. Contours of Mach number in critical areas of the flow field provide useful information on the flow characteristics.

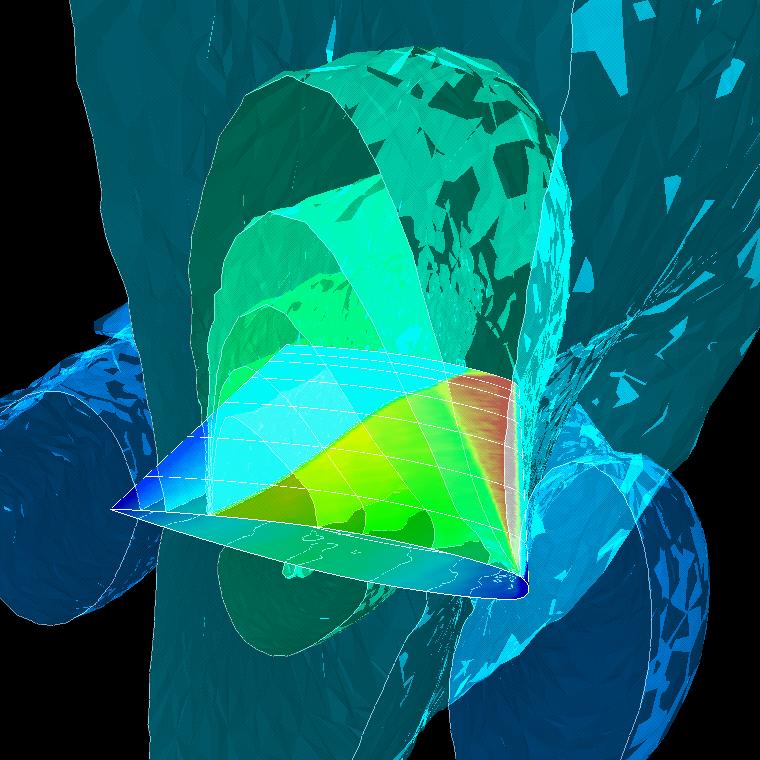
This figure, instead, shows iso-surfaces of Mach number over a M6 ONERA wing. The free-stream Mach number is 0.84, and the angle of attack 3.06. The red zone on the upper part of the wing represents a supersonic area. The sudden transition from red to green indicates the presence of a strong shock wave; moreover, the concentration of iso-surfaces behind it reveals that a further (weaker) shock wave develops.

This last figure shows the streamlines around a X29 aircraft. The starting mesh is made up of 726,713 cells and 136,787 nodes.