import matplotlib.pylab as plt
import numpy as np
import pandas as pd
from tqdm.notebook import trange
We define a class for the board. It will be used by the environment but also by the agents, because both have to know the action space and the state space. The boards has 9 positions, and for each position can be empty, marked by player 1 or marker by player 2. Therefore, in total we have $3^9$ possible positions. Therefore, the state space has size $3^9$ and the action space has size 9.
This class performs the conversion from the state space to the $i, j$ coordinates on the board, with the $i$ coordinate indicating the rows and the $j$ coordinate the columns, starting from 0 to 2.
The most important method is the play() method. It takes the action to be performed and the player (PLAYER_1_MARKER or PLAYER_2_MARKER) and performs the move. The new state state can either be a proper state (that is, a number from 0 up to NUM_STATES) or a negative number:
INVALID_MOVE_STATEindicates that the action was invalid;DRAWN_STATEindicates that the game has terminated and is a drawn;VICTORY_STATEindicates that the game has terminated and is a victory for the player.
The board is represented by an object of class TicTacToeBoard, which takes care of mapping the board as a $3 \times 3$ array of values to an state we can feed into the algorithm. Each value on the board is 0 for an empty cell, 1 if the first player has marked that cell, or 2 if the second player has marked that cell. Since each cell can have three values at most, the total number of state is $3^9 = 19683$. This includes illegal states – for example, a board with all 1’s or all 2’s. The number of legal states is about half of what we use, but it’s not an issue for this simple problem.
class TicTacToeBoard():
EMPTY_ID = 0
PLAYER_1_ID = 1
PLAYER_2_ID = 2
INVALID_MOVE_STATE = -1
DRAWN_STATE = -2
VICTORY_STATE = -3
NUM_ACTIONS = 9
NUM_STATES = 3**9
def __init__(self):
self.encoder = [3**k for k in range(9)]
self.reset()
def _get_state(self):
return np.dot(self.board.flatten(), self.encoder)
def reset(self):
# the board remembers who has to play and will complain if the wrong play() is called.
self.expected_player = self.PLAYER_1_ID;
self.done = False
self.board = np.zeros((3, 3), dtype=np.int)
return self._get_state()
def is_valid(self, action):
i = action // 3
j = action % 3
return self.board[i, j] == self.EMPTY_ID
def play1(self, action, render=False):
assert self.expected_player == self.PLAYER_1_ID
retval = self._play(action=action, player=self.PLAYER_1_ID, render=render)
self.expected_player = self.PLAYER_2_ID if retval >= 0 else None
return retval
def play2(self, action, render=False):
assert self.expected_player == self.PLAYER_2_ID
retval = self._play(action=action, player=self.PLAYER_2_ID, render=render)
self.expected_player = self.PLAYER_1_ID if retval >= 0 else None
return retval
def _play(self, *, action, player, render=False):
i = action // 3
j = action % 3
# we either return the new state if the game continues, or a negative
# number that indicates the result (invalid move, won, or drawn)
if self.board[i, j] != self.EMPTY_ID:
return self.INVALID_MOVE_STATE
self.board[i, j] = player
if render:
print('Move from player ' + ('X' if player == self.PLAYER_1_ID else 'O'))
self.render()
if self._is_winner(player):
return self.VICTORY_STATE
elif self._is_drawn():
return self.DRAWN_STATE
return self._get_state()
def _is_drawn(self):
return self.board.flatten().min() != 0
def _is_winner(self, player):
# check the rows
for i in range(3):
if self.board[i, 0] == player and self.board[i, 1] == player and self.board[i, 2] == player:
return True
# check the columns
for j in range(3):
if self.board[0, j] == player and self.board[1, j] == player and self.board[2, j] == player:
return True
# check the diagonals
if self.board[0, 0] == player and self.board[1, 1] == player and self.board[2, 2] == player:
return True
if self.board[0, 2] == player and self.board[1, 1] == player and self.board[2, 0] == player:
return True
return False
def render(self):
for i in range(3):
print("-------------")
for j in range(3):
print("|", end="")
if self.board[i,j] == self.PLAYER_1_ID:
print(" X ", end="")
elif self.board[i,j] == self.PLAYER_2_ID:
print(" O ", end="")
else:
print(" ", end="")
print("|")
print("-------------")
def get_valid_actions(self, state):
valid_actions = []
for i in range(9):
if state % 3 == self.EMPTY_ID:
valid_actions.append(i)
state = state // 3
return valid_actions
As a little test, we play a few moves and plot the board.
board = TicTacToeBoard()
print(board.play1(action=4))
print(board.play2(action=5))
print(board.play1(action=1))
print(board.play2(action=2))
assert board.play1(action=7) == board.VICTORY_STATE
board.render()
81
567
570
588
-------------
| | X | O |
-------------
| | X | O |
-------------
| | X | |
-------------
We are ready to define the agent, for which we assume that a method get_action(self, state) is available. It is straightforward to write a random agent that picks a random action all the times, with some simple
logic to avoid illegal moves.
class RandomAgent:
def __init__(self, player_id, env):
self.player_id = player_id
self.env = env
def update_epsilon(self):
# nothing to do, this is always random
pass
def update(self, state, action, reward, new_state, is_terminal):
#print("NO UPDATE")
pass
def get_action(self, state):
return np.random.choice(self.env.get_valid_actions(state))
This is instead the Q-learning agent.
class QLearningAgent:
INVALID_ACTION_VALUE = -1_000_000
def __init__(self, player_id, env, alpha, epsilon, epsilon_decay, epsilon_min):
self.player_id = player_id
self.alpha = alpha
self.epsilon = epsilon
self.epsilon_decay = epsilon_decay
self.epsilon_min = epsilon_min
self.Q = np.ones((env.NUM_STATES, env.NUM_ACTIONS)) * self.INVALID_ACTION_VALUE
for state in range(env.NUM_STATES):
valid_actions = env.get_valid_actions(state)
self.Q[state, valid_actions] = 0.0
self.N = np.zeros((env.NUM_STATES, env.NUM_ACTIONS), dtype=np.int)
self.env = env
def update_epsilon(self):
self.epsilon = max(self.epsilon * self.epsilon_decay, self.epsilon_min)
def update(self, state, action, reward, new_state, is_terminal):
self.N[state, action] += 1
alpha = self.alpha
assert self.Q[state, action] > self.INVALID_ACTION_VALUE
if is_terminal:
self.Q[state, action] += alpha * (reward - self.Q[state, action])
else:
Q_max = np.max(self.Q[new_state])
assert Q_max > self.INVALID_ACTION_VALUE
self.Q[state, action] += alpha * (reward + Q_max - self.Q[state, action])
def get_action(self, state, zero_epsilon=False):
valid_actions = self.env.get_valid_actions(state)
if np.random.uniform() < self.epsilon and not zero_epsilon:
action = np.random.choice(valid_actions)
else:
noise = 1e-8 * np.random.uniform(size=(1, 9))
action = np.argmax(self.Q[state] + noise)
return action
It is key in reinforcement learning to specify rewards in a meaningful way. A big penalty is associated with an invalid action. Playing without terminating the game doesn’t bring anything. For final states, we have zero reward for a drawn, one for victory and minus one for a lost game.
INVALID_ACTION_REWARD = -1000.0
CONTINUE_REWARD = 0.0
LOST_REWARD = -1.0
DRAWN_REWARD = 0.0
VICTORY_REWARD = 1.0
def play_game():
state = board.reset()
while True:
action = p1.get_action(state, zero_epsilon=True)
state = board.play1(action)
if state == TicTacToeBoard.DRAWN_STATE:
return 0
elif state == TicTacToeBoard.VICTORY_STATE:
return 1
action = p2.get_action(state, zero_epsilon=True)
state = board.play2(action)
if state == TicTacToeBoard.DRAWN_STATE:
return 0
elif state == TicTacToeBoard.VICTORY_STATE:
return 2
return False
What we do here is to let two Q-learning agents play against each other. Agent p1 learns how to play as first player, while agent p2 learns how to play the second player. We keep a quite large exploration rate of 0.5 to ensure that we don’t get stuck into local minima. Every one thousand training games, we play the two agents against each other without any randomness, that is using the optimal strategy.
np.random.seed(0)
board = TicTacToeBoard()
p1 = QLearningAgent(TicTacToeBoard.PLAYER_1_ID, board, alpha=0.1, epsilon=1, epsilon_decay=0.9999, epsilon_min=0.5)
p2 = QLearningAgent(TicTacToeBoard.PLAYER_2_ID, board, alpha=0.1, epsilon=1, epsilon_decay=0.9999, epsilon_min=0.5)
results = []
for i in trange(1_000_000):
states = [board.reset()]
actions = []
current_player = p1
previous_player = p2
while True:
action = current_player.get_action(states[-1])
state = board.play1(action, render=False) if current_player.player_id == 1 else board.play2(action, render=False)
assert state != TicTacToeBoard.INVALID_MOVE_STATE
states.append(state)
actions.append(action)
if state == TicTacToeBoard.DRAWN_STATE:
current_player.update(states[-2], actions[-1], DRAWN_REWARD, None, True)
previous_player.update(states[-3], actions[-2], DRAWN_REWARD, None, True)
break
elif state == TicTacToeBoard.VICTORY_STATE:
current_player.update(states[-2], actions[-1], VICTORY_REWARD, None, True)
previous_player.update(states[-3], actions[-2], LOST_REWARD, None, True)
break
# the player cannot lose on his or her move, and no invalid action can be performed
if len(states) > 2:
previous_player.update(states[-3], actions[-2], CONTINUE_REWARD, states[-1], False)
current_player, previous_player = previous_player, current_player
p1.update_epsilon()
p2.update_epsilon()
if i % 1000 == 0:
results.append(play_game())
HBox(children=(HTML(value=''), FloatProgress(value=0.0, max=1000000.0), HTML(value='')))
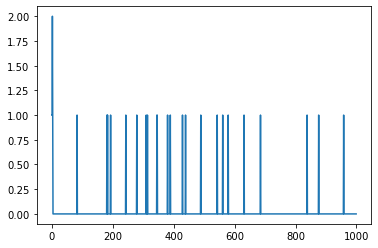
We can plot the winners – p2 wins only at the beginning, then it is either drawn or p1. We would expect most of the games to be drawn, as it is easy to master the game and avoid defeats.
plt.plot(results)
[<matplotlib.lines.Line2D at 0x1f36666a070>]
It is also nice to plot the Q matrix for the first state of p1. Theory says that the best action of p1 would be to select (0, 0), however it seems that all other choices aren’t too bad, probably because it is so easy to always end up in a drawn game.
def print_Q(agent, observation):
Q = agent.Q[observation].reshape(3, 3)
Q_max = Q.max().max()
for i in range(3):
for j in range(3):
entry = Q[i, j]
if entry == agent.INVALID_ACTION_VALUE:
print('#### ', end='')
else:
print(f'{entry / Q_max:.2f} ', end='')
print()
print('scaled Q matrix for the initial state for p1:')
print_Q(p1, 0)
scaled Q matrix for the initial state for p1:
0.97 0.95 0.88
0.84 1.00 0.86
0.91 0.89 0.89
The response of p2 to the initial move of (0, 0) is more clear – p2 should select the cell at the center, and it does.
obs = board.reset()
obs = board.play1(0)
print('Q matrix after best first action for p2:')
print_Q(p2, obs)
Q matrix after best first action for p2:
#### 0.00 0.70
-0.11 1.00 0.65
0.24 0.59 0.02
Finally, we play against the computer, we start first.
class HumanAgent:
def __init__(self, player_id):
self.player_id = player_id
def get_action(self, observation):
choice = input(f'{self.player_id} move (i, j) = ')
tokens = choice.split(',')
i, j = int(tokens[0]), int(tokens[1])
return i * 3 + j
p1 = HumanAgent(2)
p2.epsilon = 0.0
state = board.reset()
while True:
action = p1.get_action(state)
state = board.play1(action)
if state < 0:
break
action = p2.get_action(state)
state = board.play2(action)
board.render()
if state < 0:
break
board.render()
2 move (i, j) = 1, 1
-------------
| | | O |
-------------
| | X | |
-------------
| | | |
-------------
2 move (i, j) = 2, 0
-------------
| | | O |
-------------
| | X | |
-------------
| X | | O |
-------------
2 move (i, j) = 1, 2
-------------
| | | O |
-------------
| O | X | X |
-------------
| X | | O |
-------------
2 move (i, j) = 0, 0
-------------
| X | | O |
-------------
| O | X | X |
-------------
| X | O | O |
-------------
2 move (i, j) = 0, 1
-------------
| X | X | O |
-------------
| O | X | X |
-------------
| X | O | O |
-------------
state == TicTacToeBoard.DRAWN_OBSERVATION
True
To conclude, this isn’t a particularly interesting game, and the Q-learning method doesn’t shine too much neither. It is interesting as a simple example of a two-player game, where moving from one state to the next means waiting for the other player’s response.